馬可夫鏈

簡介

「馬可夫鏈」是一種具有狀態的隨機過程，有點像是「有限狀態機」，但是「從目前狀態轉移 s 到下一個狀態 s’ 的機率」由 $Q(s \to s')$ 所表示，這個狀態之轉移機率並不會受到狀態以外的因素所影響，因此與時間無關。

隨機漫步就是馬可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點，每一步可以移動到任何一個相鄰的點，在這裡移動到每一個點的概率都是相同的(無論之前漫步路徑是如何的)。

假如我們不斷的觀察某種隨機現象，會看到許多一連串的觀察值 $x_1, x_2,..., x_n$ ，這些觀察值會形成整個隨機現象空間 $X_1, X_2,..., X_n$。

假如這些觀察值之間有某種因果關係，那麼我們就有可能透過馬可夫過程描述此因果關係，舉例而言，如果每個事件只受到前一個事件的影響，那麼就可以用 $P(X_{n+1} | X_n)$ 表示此隨機現象，這種隨機過程稱為時間無關的馬可夫鏈 (Time-homogeneous Markov chains, 或稱為穩定型馬可夫鏈 stationary Markov chains)。

假如下一個觀察值可能受前 m 個觀察值所影響，那麼此種隨機過程可由機率分布 $P(X_{n+1} | X_n, ..., X_{n-m+1})$ 表示，因此稱為 m 階的馬可夫過程。

馬可夫系統的範例

對於一個具有「馬可夫特性」的「機率式有限狀態機」，我們可以用「機率轉移矩陣」進行描述，舉例而言：下圖顯示了一個只有兩個狀態的「馬可夫隨機系統」。

若要用機率模型描述上述兩個狀態的馬可夫系統，我們需要給定兩組機率值，第一組是狀態本身的機率 P(s0)、P(s1)。第二組是狀態轉移的機率 Q(s0→s0)、Q(s0→s1)、Q(s1→s0)、Q(s1→s1)。

長期來看、馬可夫系統通常最後會達到一個穩定平衡，在平衡的情況之下，每個節點的輸出將會等於該節點的輸入，這就是所謂的「一般平衡條件」。

馬可夫系統的一般平衡條件

讓我們用下圖的範例來說明「馬可夫系統」達到穩定平衡時的狀況。

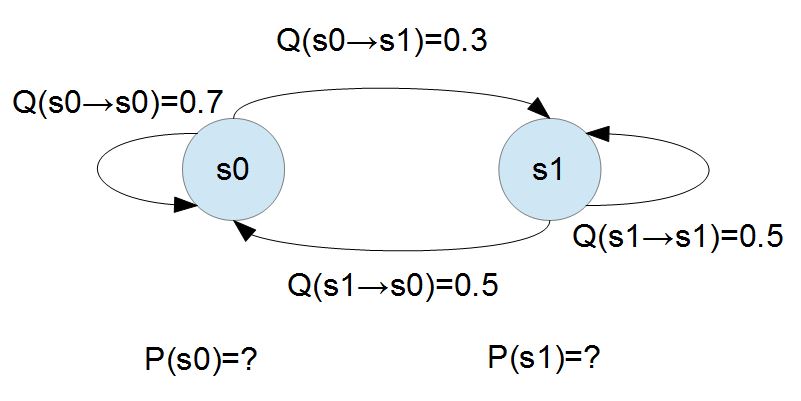
對於上述有「馬可夫隨機系統」，我們可以用「二元一次聯立方程式」求解 P(s0) 與 P(s1)，假如我們將 P(s0) 寫為 P0，P(s1) 寫為 P1，那麼整個系統達到平衡時，應該會有下列狀況。

P0*0.3 = P1*0.5 ; P0 的流出量 = P0 的流入量
P0+P1 = 1       ; 狀態不是 s0 就是 s1

如果我們求解上述方程式，就可以得到 (P0=5/8, P1=3/8)，此時整個系統會達到平衡。

假如我們模擬機率性粒子在馬可夫鏈中的移動行為，最後這些移動將達到一個平衡。在達到平衡後，從 x 狀態流出去的粒子數，將會等於流回該狀態的粒子數，也就是必須滿足下列『平衡條件』的要求。

\sum_y P(x) Q(x \to y)  = \sum_y P(y) Q(y \to x)

當隨機的粒子移動時，如果從 x 流出的粒子較多，自然會讓 P(x) 下降，最後仍然達到平衡，如果流入 x 的粒子比流出的多，那麼 P(x) 自然就會上升，只要我們能模擬流出流入的程序，最後整個馬可夫系統將會達到平衡。

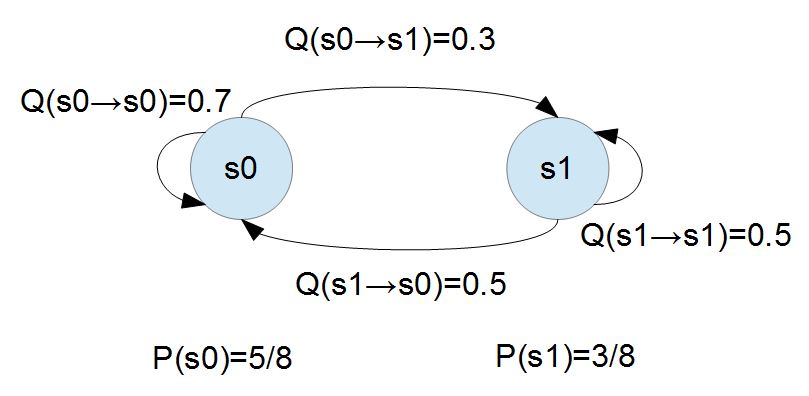
上圖顯示了上述馬可夫系統處於「一般平衡狀態」時的狀況，您可以發現其中的「節點 s0 的總流出」為 $(5/8*0.3 = 15/80)$ ，而「節點 s0 的總流入」$(3/8*0.5 = 15/80)$，其計算過程如下所示。

\sum_y P(x) Q(x \to y) = 5/8 * 0.3 = 15/80 = 3/8*0.5 = \sum_y P(y) Q(y \to x)

運用上述的「一般平衡條件」，當我們已經知道「轉移矩陣」$Q(x \to y)$ 的每個數值，但是卻不知道達成平衡的節點機率 P(x) 時，可以設計出一種稱為 「Gibbs 演算法」的學習程式，該算法可以尋找出每個節點達到平衡時的機率值。

馬可夫系統的細緻平衡條件

在上述兩個狀態的馬可夫系統中，對於 s0 與 s1 之間的兩條連線， $s0 \to s1$ 與 $s1 \to s0$ 而言，其實已經達到了所謂細緻均衡的條件，因為

P(s0)*Q(s0 \to s1) = 5/8 * 0.3 = 15/80 = 3/8*0.5 = P(s1)*Q(s1 \to s0)

假如一個「馬可夫系統」裏的每條線都能達成這樣的平衡，那麼整個系統顯然也是處於一個穩定狀態。這種架構在「線平衡」上的均衡條件，稱為「細致平衡條件」，以下是「細致平衡條件」的數學方程式。

P(x) Q(x \to y)  = P(y) Q(y \to x)

必須注意的是，上述的「細致平衡條件」是比「一般平衡」更進一步，要求更多的條件，因此若能達到「細致平衡」，則必然已經達到了「一般平衡」狀態。

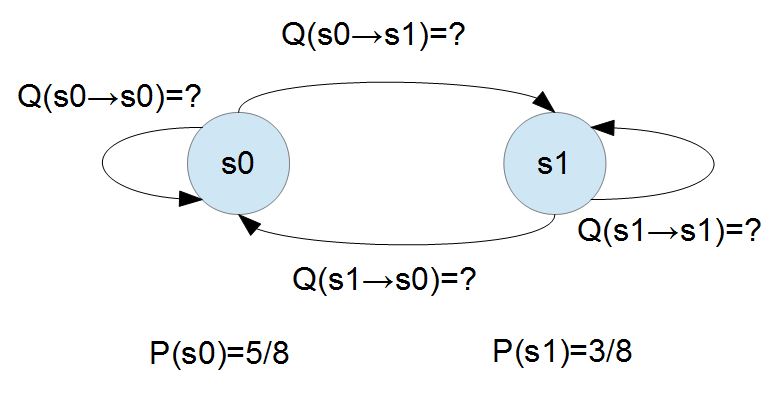
當我們知道每個狀態的機率 P(x)，卻不知道「轉移矩陣」的機率值時，就可以採用「細緻平衡的要求」，透過「Metropolis-Hasting 演算法」來學習，以便透過反覆的疊代運算找出讓 $Q(x\to y)$ 達成平衡的數值，透過迭代的方式學會「轉移矩陣」的機率值。

蒙地卡羅馬可夫 (MCMC) 算法

在上述的馬可夫系統中，我們若想要尋找他的穩定狀態，也就是 P(s0)=?, P(s1)=? 才能讓整個系統達到平衡的問題，我們可以採用「蒙地卡羅」 (Monte Carlo) 演算法，而採用「蒙地卡羅」型態的演算法解決馬可夫鏈問題，就稱為 MCMC (Monte Carlo Markov Chain)。

「Gibbs 演算法」與 「Metropolis Hasting 演算法」都是典型的 MCMC 算法。

其中的 「Gibbs 演算法」是在「已知轉移矩陣」時可用來「求解各個節點的機率」，而 「Metropolis Hasting 演算法」 則是在「已知各個節點的機率」時，可以用來學習「求解轉移矩陣的機率」。