Alpha-Beta 修剪法
您可以看到 Min-Max 對每個節點都進行遞迴展開,這種展開的數量是很龐大的,因此即使電腦非常快也展開不了幾層,所以我們必須透過「Alpha-Beta 修剪法」減少展開的數量,以下是一個範例。
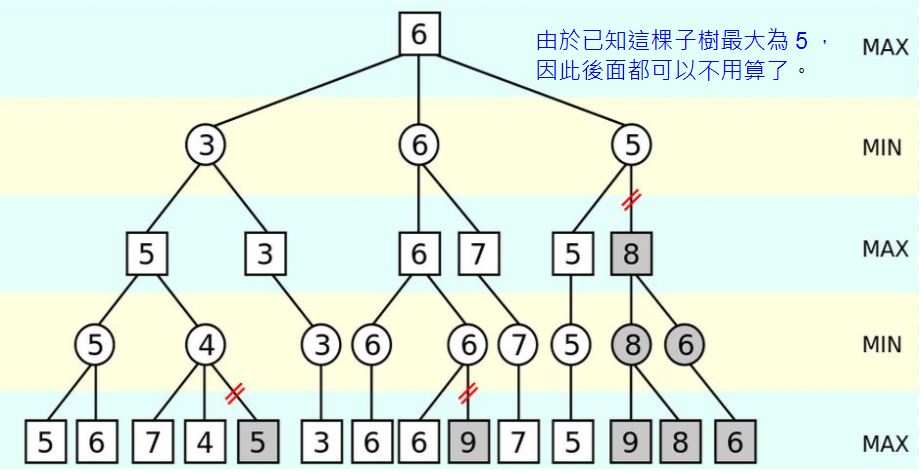
在上圖中,請注意上面 Min 層的 5 節點,您可以看到當該節點最左邊子樹的分數 5 已經計算出來後,由於 5 比 8 還小,因此不管後面的節點分數為多少,都不可能讓其父節點變得比 5 還要大,所以右邊的子樹都可以不用再計算了,這就是 Alpha-Beta 修剪法的原理。
「Alpha-Beta 修剪法」其實是「Min-Max 對局搜尋法」的一個修改版,主要是在 Min-Max 當中加入了 α 與 β 兩個紀錄值,用來做為是否要修剪的參考標準,演算法如下所示。
function alphabeta(node, depth, α, β, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
for each child of node
α := max(α, alphabeta(child, depth - 1, α, β, FALSE))
if β ≤ α
break (* β cut-off *)
return α
else
for each child of node
β := min(β, alphabeta(child, depth - 1, α, β, TRUE))
if β ≤ α
break (* α cut-off *)
return β
(* Initial call for maximizing player *)
alphabeta(origin, depth, -∞, +∞, TRUE)
結語
當然、 Alpha-Beta 修剪法並不保證能將對局樹修剪得非常小,而且樹的大小會與拜訪的順序有關,如果希望樹可以比較小的話,應當從「對我方分數最高、對敵方分數最低」的節點開始處理,這樣才能有效的降低整棵對局搜尋樹的大小。
參考文獻
【本文由陳鍾誠取材並修改自 [維基百科],採用創作共用的 [姓名標示、相同方式分享] 授權】