Min-Max 對局搜尋法

雖然我們在前文設計五子棋程式時單純使用了盤面評估函數就已經設計出了「具備自動下棋能力的電腦程式」，但是這種設計方法是不夠強大的。

電腦下棋要夠強大，通常必須採用「Min-Max 對局搜尋法」，如果能夠搜尋得愈深，電腦的棋力通常就會越高。

但是、對於電腦而言，每一層都有很多可能的下法，對手也可能會有很多的回應方式，這樣一層一層下去會有組合爆炸的問題。

舉例而言，假如對上文中有 256 格的棋盤而言，第一子的下法有 256 種，第二子的下法就有 255 種，….

因此若我們要進行 n 層的徹底搜尋，那在下第一步之前就必須探詢 256255…*(256-n+1) 這麼多種可能性，當 n 超過 10 層時，幾乎任何電腦都不可能在短短數秒內完成這樣的搜尋。

於是我們就必須減少蒐尋的可能性，這時我們可以採用著名的「 Alpha-Beta Cut」修剪法來減少蒐尋的空間大小。

讓我們先來瞭解一下何謂 「Min-Max 對局搜尋法」。

在下棋的時候，如果要打敗對手，必須考量讓自己得分最多，且讓對手得分最少，Min-Max 正是根據這樣的想法而設計出來的。

必須注意的是，當電腦要下一子之前，當然會下讓自己得分最多的那一格，但是這很容易會落入對手的陷阱，因為得分最多的那一格很可能接下來失分更多。

於是、一個合理的想法是將所有層次分為「敵我雙方」兩類，我方下的那層得分越多越好，而對方下的那層失分越少越好。

而且、我們不能假設對方是個笨蛋，因此在每一層上，我們都必須認為「對方可能會下出讓我們失分最多的一步」，而我們必須盡可能選擇「最大失分最小化」的策略，這種想法就導出了「Min-Max 對局搜尋法」，以下是一個範例。

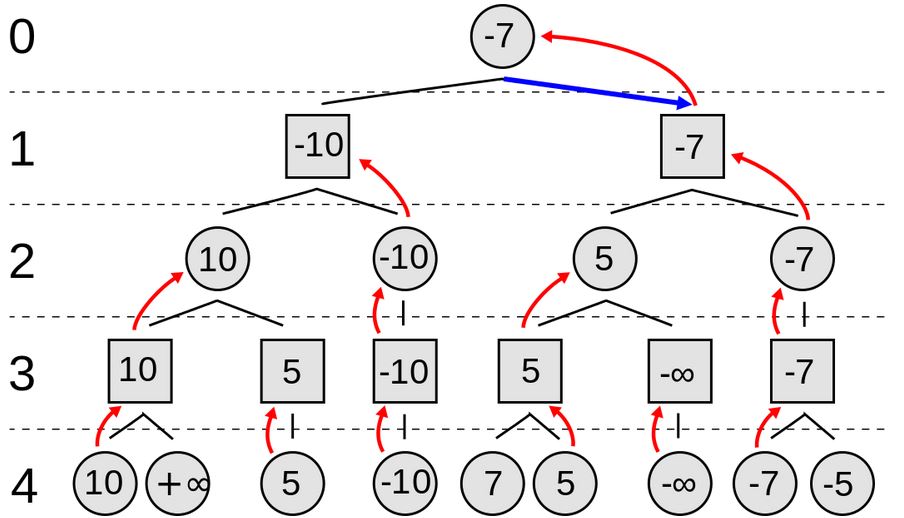
在上圖中、由於第 0 層代表我方下，所以我們取在第一層失分少的步驟，而第 1 層代表敵方下，所以假設他們也會採取對他們最有利的下法 (也就是對我們最不利的、讓我們失分多的) ，整張圖的推論邏輯就在這種 Min-Max 的過程中完成了。

必須補充說明的是，圖中的 -∞ 與 +∞ 通常代表該節點為樹葉節點，也就是整盤棋已經結束。換句話說、有人輸了或贏了。

演算法： Min-Max 對局搜尋

function minimax(node, depth, maximizingPlayer)
    if depth = 0 or node is a terminal node
        return the heuristic value of node
    if maximizingPlayer
        bestValue := -∞
        for each child of node
            val := minimax(child, depth - 1, FALSE))
            bestValue := max(bestValue, val);
        return bestValue
    else
        bestValue := +∞
        for each child of node
            val := minimax(child, depth - 1, TRUE))
            bestValue := min(bestValue, val);
        return bestValue

(* Initial call for maximizing player *)
minimax(origin, depth, TRUE)