反傳遞算法
如前文所述,《梯度下降法》是《深度學習神經網路》背後的學習算法,但是再輸入變數很多時,純粹靠《多次前向計算》的《梯度下降法》速度會過慢,因此我們需要使用《反傳遞算法》更有效率的計算《梯度》。
節點 Node
反傳遞算法是用來快速計算神經網路中梯度的方法,方法是把每個變數都變成一個具有(值 v + 梯度 g) 的節點 (node),其結構如下:
class Node {
constructor(v = 0, g = 0) {
this.v = v // 輸出值 (f(x))
this.g = g // 梯度值 (偏微分)
}
}
閘 Gate
神經網路中的每個運算,都被表示成一種閘 (Gate),這些閘可以進行正向 forward 計算,也可以反向 backward 傳遞梯度,以下是 Gate 的類別定義。
class Gate {
constructor(o, x, y, f, gfx, gfy) {
this.p = {o:o, x:x, y:y, f:f, gfx:gfx, gfy:gfy||gfx} // 當 gfy 沒設定時,就代表 gfy = gfx
}
forward() {
let p = this.p
p.o.v = p.f(p.x.v, p.y.v)
}
backward() {
let p = this.p
p.x.g = p.gfx(p.o.v)
p.y.g = p.gfy(p.o.v)
}
}
對於每個 gate ,函數 f 是用來進行《正向傳遞》forward() 計算的。
舉例而言,我們可以使用以下指令定義一個乘法閘 gmul
// f gfx gfy
let gmul = new Gate(o, x, y, (x,y)=>x*y, (x,y)=>y, (x,y)=>x))
其中的 f(x,y)=>x*y 是 gmul 的正向計算函數,會計算出 o.v = x.v * y.v 的結果,放在節點 o 中。
而 gfx(x,y)=>y 與 gfy(x,y)=>x 是 gmul 的反向計算函數,會根據 o 節點的《值與梯度》 (o.v, o.g) 反向計算出 x, y 的梯度 x.g 與 y.g 。
前向計算函數 f 是個乘法閘 f(x,y)=x*y,應該很容易理解。但是反向計算函數 gfx 與 gfy 為何是 gfx(x,y)=>y 與 gfx(x,y)=>x 呢?
反傳遞的原理
梯度的反向傳遞原理在 Andrej Karpathy 的 Hacker’s guide to Neural Networks 一文中有詳盡的說明,讓我們在此簡述其精要。
對於 f(x,y) = xy 而言,假如 f 的梯度為 f.g ,那麼由於:
\frac{\partial{f(x,y)}}{\partial{x}} = \frac{\partial{xy}}{\partial{x}} = y
因此 x 的梯度應該是 x.g = y * f.g。
同理、 y 的梯度 y.g = x * f.g 。
所以只需要知道 f.g 與 f(x,y)=xy,就可以逆向推出 x.g 與 y.g。
這就是所謂的《梯度反傳遞》。
而這也是為何上述程式中 gfx(x,y)=>y 與 gfy(x,y)=>x 的原因。
讓我們考慮一個更複雜的兩層式網路如下圖,該網路是計算 f = (x+y) * z 這個算式。
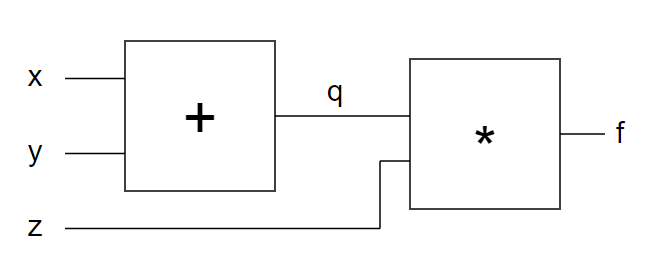
其中的 q = x+y, 而 f = q*z。
根據偏微分的鏈鎖規則,我們可以用以下數學式描述 f, q, x 之間的梯度關係。
\frac{\partial{f(q,z)}}{\partial{x}} = \frac{\partial{q(x,y)}}{\partial{x}} \frac{\partial{f(q,z)}}{\partial{q}}
由於 f 為輸出,我們可以先將 f 的梯度 f.g 設定為 1,那麼就可以推斷其他變數的梯度值。
(註:其實輸出 f.g 可以設為一的非零值,代表梯度下降的移動長度,對於有《樣本與標準答案》的學習,可以將 f.g 設為輸出與標準答案的差距)
\frac{\partial{f(q,z)}}{\partial{q}} = \frac{\partial{qz}}{\partial{q}} =z
x.g = \frac{\partial{f(q,z)}}{\partial{x}} = \frac{\partial{f(q,z)}}{\partial{q}} \frac{\partial{q(x,y)}}{\partial{x}}=\frac{\partial{qz}}{\partial{q}} \frac{\partial{x+y}}{\partial{x}}=z*1
因此當 f.g 已知的時候,我們可以算出 q.g ,由於 f = q*z ,因此 q 的梯度 q.g = z*f.g (當 f.g = 1 時,則 q.g = z)。
接著我們可以透過 q=x+y 來計算 x 的梯度,得到 x.g=q.g*f.g 來計算 x 的梯度 x.g ,於是同樣得到 x.g=z*f.g (因為 $\frac{\partial{q}}{\partial{x}}=\frac{\partial{x+y}}{\partial{x}}=1$ )。
經由這種反傳遞的方式,我們就能從輸出端一路到推回中間層、然後再推回輸入端,計算出每個節點的梯度。
網路 Net
透過這些 Node + Gate 的組合,我們可以設計出能計算任何函數的神經網路 Net。
舉例而言,以下網路 net 會計算 $x^2+y^2$ ,其輸出結果會放在節點 o 當中。
const net = new nn.Net()
let x = net.variable(2)
let y = net.variable(1)
let x2 = net.mul(x, x)
let y2 = net.mul(y, y)
let o = net.add(x2, y2)
我們只要呼叫網路的正向傳遞函數 net.forward() 就能從輸入值開始,經過每個閘的前向傳遞 gate.forward() 計算出結果 。
class Net {
constructor () {
this.gates = []
}
variable (v, g) {
return new Node(v, g)
}
op (x, y, f, gfx, gfy) {
let o = new Node()
let g = new Gate(o, x, y, f, gfx, gfy)
this.gates.push(g)
this.o = o
return o
}
add (x, y) { return this.op(x, y, (x,y)=>x+y, (x,y)=>1) }
mul (x, y) { return this.op(x, y, (x,y)=>x*y, (x,y)=>y, (x,y)=>x) }
forward() { // 正向傳遞計算結果
for (let gate of this.gates) {
gate.forward()
}
return this.o
}
backward() { // 反向傳遞計算梯度
this.o.g = 1 // 設定輸出節點 o 的梯度為 1
for (let i=this.gates.length-1; i>=0; i--) { // 反向傳遞計算每個節點 Node 的梯度 g
let gate = this.gates[i]
gate.backward()
}
}
watch (nodes) {
this.nodes = nodes
}
dump() {
return this.nodes
}
}
當我們想知道該網路的輸入 (x,y) 應該調整多少,才能朝梯度方向前進時,我們只要呼叫 net.backward() ,就能透過反向傳遞計算出每個節點的梯度。
程式執行
有了上述概念後,讓我們來看個範例好了,以下這個網路是計算 $o=x^2+y^2$ 的函數,我們希望能透過《梯度下降+反傳遞算法》找出其最低點。
檔案: f.js
const nn = require('../../nn')
const net = new nn.Net()
let x = net.variable(2)
let y = net.variable(1)
let x2 = net.mul(x, x)
let y2 = net.mul(y, y)
let o = net.add(x2, y2)
net.watch({x,y,x2,y2,o})
module.exports = new nn.FNet(net, {x:x, y:y})
該程式的主程式很簡單,只是對該網路呼叫梯度下降法進行優化而已。
檔案: optimizeEx.js
const nn = require('../../nn')
const f = require('./f')
nn.optimize(f, {x:1, y:1})
執行的結果如下:
$ cd example/02-backprop
$ node .\gradientEx
p= {x:2.0000, y:1.0000} f(p)= 5
gp= { x: 4, y: 1 }
p= {x:1.9600, y:0.9900} f(p)= 4.8217
gp= { x: 3.8415999999999997, y: 0.9801 }
p= {x:1.9216, y:0.9802} f(p)= 4.653275148657
gp= { x: 3.692485069056, y: 0.960790079601 }
p= {x:1.8847, y:0.9706} f(p)= 4.493987190929792
gp= { x: 3.5519401090757823, y: 0.9420470818540095 }
// ... 中間省略 ....
p= {x:0.0479, y:0.0467} f(p)= 0.004475389263812065
gp= { x: 0.00228988872537307, y: 0.0021855005384389947 }
p= {x:0.0478, y:0.0467} f(p)= 0.004471155300865204
gp= { x: 0.002287697698821976, y: 0.0021834576020432284 }
p= {x:0.0478, y:0.0467} f(p)= 0.004466927345179781
gp= { x: 0.002285509815916863, y: 0.002181417529262918 }
上述程式最後找到了 p={x:0.0478, y:0.0467} 這個非常接近 (0,0) 的點,正確地找到了函數 $x^2+y^2$ 的最低點 f(0,0)=0。
現在、您應該已經可以理解《梯度下降法與反傳遞算法》的運作原理了。
雖然《反傳遞算法》早在 1963 年就由 Vapnik 提出了,但是卻直到 1986 年時才由於 Hinton 等人在語音辨識上的實作成果而引發注意。
接著《神經網路》又沉寂了十幾年,到了 2011 年 Hinton 的學生用 CNN 捲積神經網路在影像辨識大賽中用 GPU 加速而大勝,再次導致神經網路進化為深度學習而爆紅。
而這一切背後運作的《反傳遞算法》,經歷了整整一甲子,並沒有多大的改變,只要您理解了這個算法的原理,就能輕鬆踏進《深度學習的神經網路領域》了!