梯度下降法
深度學習 (Deep Learning) 是人工智慧領域當紅的技術,說穿了其實就是原本的《神經網路》(Neural Network) ,不過由於加上了一些新的模型 (像是捲積神經網路 CNN, 循環神經網路 RNN 與生成對抗網路 GAN),還有在神經網路的層數上加深很多,從以往的 3-4 層,提升到了十幾層,甚至上百層,於是我們給這些新一代的《神經網路》技術一個統稱,那就是《深度學習》。
雖然《深度學習》的神經網路層數變多了,《網路模型》也多了一些,但是背後的學習算法和運作原理並沒有多大改變,仍然是以《梯度下降》(Gradient Descendent) 和《反傳遞算法》(Back Propagation) 為主。
但是《梯度下降》和《反傳遞算法》兩者,幾乎都是以數學的形式呈現,其中《梯度》的數學定義如下:
\nabla_{x} f(x) = \left[ \frac{\partial }{\partial x_1} f(x), \frac{\partial }{\partial x_2} f(x),\cdots,\frac{\partial }{\partial x_n} f(x) \right]^T=\frac{\partial }{\partial{x}} f(x)
若把《梯度》當成一個《巨型算子》可以寫為如下形式:
\nabla_{x} = \left[ \frac{\partial }{\partial x_1}, \frac{\partial }{\partial x_2},\cdots,\frac{\partial }{\partial x_n} \right]^T=\frac{\partial }{\partial{x}}
這樣的數學雖然只是《基本的偏微分》,但是卻足以嚇倒很多人,包括我在內!
《反傳遞算法》的運作原理,則是建築在《微積分的鏈鎖規則》上,如以下算式所示:
\frac{\partial{f(q,z)}}{\partial{x}} = \frac{\partial{q(x,y)}}{\partial{x}} \frac{\partial{f(q,z)}}{\partial{q}}
根據這兩個數學式,人工智慧領域發展出了一整套《神經網路訓練算法》,稱為《反傳遞算法》,可以用來訓練《神經網路》,讓程式可以具有《函數優化》的能力。
有了函數優化的能力,程式就能向《一群樣本與解答》學習,優化《解答的能力》,進而解決《手寫辨識、語音辨識、影像辨識》甚至是《機器翻譯》等問題。
如果我們有個函數能計算《錯誤率》,那麼透過《優化算法》,我們就能找到讓錯誤率很低的函數,這個錯誤率很低的函數,就很少會在《訓練學習樣本》上回答錯誤。
如果這個函數還具有《通用延展性》,也就是在《非學習樣本上》也表現得同樣良好,那麼這個函數基本上就解決了該問題。
在本文中,我們將從《梯度下降法》開始,讓熟悉程式的人能夠輕易的透過《程式》來理解《深度學習背後的那些數學》!
梯度
如前所述,《梯度》的數學定義如下:
\nabla_{x} f(x) = \left[ \frac{\partial }{\partial x_1} f(x), \frac{\partial }{\partial x_2} f(x),\cdots,\frac{\partial }{\partial x_n} f(x) \right]^T=\frac{\partial }{\partial{x}} f(x)
問題是、這樣的數學符號對程式人有點可怕,到底梯度有甚麼直覺意義呢?讓我們看看下圖:
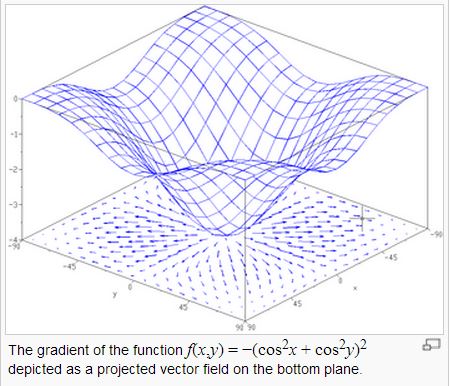
其實梯度就是斜率最大的那個方向,所以梯度下降法,其實就是朝著斜率最大的方向走。
如果我們朝著《斜率最大》方向的《正梯度》走,那麼就會愈走愈高,但是如果朝著《逆梯度》方向走,那麼就會愈走愈低。
而梯度下降法,就是朝著《逆梯度》的方向走,於是就可以不斷下降,直到到達梯度為 0 的點 (斜率最大的方向仍然是斜率為零),此時就已經到了一個《谷底》,也就是區域的最低點了!
理解了這個直覺概念之後,我們的下一個問題是,如何用程式來計算《梯度》呢?
其實、很多數學只要回到基本定義,就一點都不可怕了!
讓我們先回頭看看梯度中的基本元素,也就是偏微分,其定義是:
\frac{\partial }{\partial x_1} f(x) = \lim_{h \to 0} \frac{f(x_1, ..., x_i+h, ...., x_n)-f(x_1, ..., x_i, ...., x_n)}{h}
舉例而言,假如對 $f(x,y) = x^2+y^2$ 這個函數而言,其對 x 的偏微分就是:
\frac{\partial }{\partial x} f(x,y) = \lim_{h \to 0} \frac{f(x+h,y)-f(x,y)}{h}
而對 y 的偏微分就是:
\frac{\partial }{\partial y} f(x,y) = \lim_{h \to 0} \frac{f(x,y+h)-f(x,y)}{h}
於是我們可以寫一個函數 df 來計算偏微分:
// 函數 f 對變數 k 的偏微分: df(p) / dk
nn.df = function (f, p, k) {
let h = nn.step
let p1 = nn.clone(p)
p1[k] += h
return (f(p1) - f(p)) / h
}
這樣我們就可以用下列指令計算出 f(x,y) 在 (1,1) 這點的偏導數:
nn.df(f, {x:1, y:1}, 'x')
只要我們對每個變數都取偏導數,然後形成一個向量,就能計算出《梯度》了! 其 JavaScript 程式如下:
// 函數 f 在點 p 上的梯度 ∇f(p)
nn.grad = function (f, p) {
let gp = {}
for (let k in p) {
gp[k] = nn.df(f, p, k) // 對變數 k 取偏導數後,放入梯度向量 gp 中
}
return gp
}
於是我們可以用 grad() 下列程式計算 f 在 (1,1) 這點的梯度。
nn.grad(f, {x:1, y:1})
假如我們定義函數 f 為 $f(x,y) = x^2+y^2$ ,那麼 f 在 (1,1) 的梯度將會是 (2x, 2y) = (2,2)。
讓我們用程式實作一下,並驗證看看梯度的計算是否正確:
先定義函數 $f(x,y) = x^2+y^2$
module.exports = function f (p) {
let x = p.x, y = p.y
return (x * x + y * y)
}
然後呼叫我們的示範套件 nn,看看其計算結果是否正確:
const nn = require('../../nn')
const f = require('./f')
console.log('df(f(x:1,y:1), x) = ', nn.df(f, {x:1, y:1}, 'x'))
console.log('grad(f(x:1,y:1))=', nn.grad(f, {x:1, y:1}))
執行結果如下:
$ node .\gradientEx.js
df(f(x:1,y:1), x) = 2.010000000000023
grad(f(x:1,y:1))= { x: 2.010000000000023, y: 2.010000000000023 }
您可以看到《偏微分與梯度》的計算,基本上都非常接近,所以是正確的。
梯度下降法
只要能計算梯度,那麼要實作《梯度下降法》就很容易了,我們可以呼叫上述的梯度函數 nn.grad(f, p) ,輕而易舉地設計出《梯度下降法》程式如下:
// 使用梯度下降法尋找函數最低點
nn.optimize = function (f, p0) {
let p = nn.clone(p0)
while (true) {
console.log('p=', pv.str(p), 'f(p)=', f(p))
let gp = nn.grad(f, p) // 計算梯度 gp
let norm = pv.norm(gp) // norm = 梯度的長度 (步伐大小)
if (norm < 0.00001) { // 如果步伐已經很小了,那麼就停止吧!
break
}
let gstep = pv.mul(gp, -1 * nn.step) // gstep = 逆梯度方向的一小步
p = pv.add(p, gstep) // 向 gstep 方向走一小步
}
return p // 傳回最低點!
}
然後讓我們測試看看,該算法是否能找到 $f(x,y) = x^2+y^2$ 的最低點。
$ node .\gradientDescendent.js
p= {x:1.0000, y:1.0000} f(p)= 2
p= {x:0.9799, y:0.9799} f(p)= 1.920408019999999
p= {x:0.9602, y:0.9602} f(p)= 1.8439757616079993
p= {x:0.9409, y:0.9409} f(p)= 1.7705779422643224
p= {x:0.9220, y:0.9220} f(p)= 1.7000942437503355
p= {x:0.9034, y:0.9034} f(p)= 1.6324091155375082
..中間省略 ...
p= {x:-0.0038, y:-0.0038} f(p)= 0.000029193378572034838
p= {x:-0.0038, y:-0.0038} f(p)= 0.00002955498084296176
p= {x:-0.0039, y:-0.0039} f(p)= 0.000029911510462712392
p= {x:-0.0039, y:-0.0039} f(p)= 0.000030262983372298253
結果果然找到 (x,y)=(0, 0) 這個最低點的區域,因此上述的方法,基本上就已經實作出《梯度下降法》了。
以上的程式放在下列 github 專案當中,透過閱讀程式碼,您應該會進一步理解完整的程式寫法。
梯度下降法的缺點
以上的《梯度下降法》,是採用計算 $\frac{f(x+h, y) - f(x, y)}{h}$, $\frac{f(x, y+h) - f(x, y)}{h}$ 這樣的方式,重複呼叫 f 幾次後達成的。
假如函數 f 的參數有 n 個,那麼要算出梯度,就必須重複的呼叫 n 次以上的 f 函數,因為至少要計算 $f(x_1+h, ....), f(x_1, x_2+h, ....), .... f(x_1, x_2, ..., x_n+h)$ 。
這樣當參數數量 n 很大的時候,梯度的計算就會變得很慢,因此我們必須想辦法加速《梯度的計算速度》。
而《反傳遞演算法》,就是用來加速《梯度計算》的一種方法,這種方法依靠的是《自動微分》功能,想辦法從後面一層的差值,計算出前面一層應該調整的方向與大小。