幾何學
幾何學在電腦裡的用途
幾何圖形的用途 ,從《計算機圖學》到《人工智慧》領域無所不在
舉例而言 ,人工智慧裡的爬山演算法 ,主要是在尋找《函數最高點》 https://mdbookspace.com/view/ai/chapter2.md
方法非常簡單,就是一直往更高的方向爬 https://mdbookspace.com/view/ai/hillClimbingMax.md
而神經網路裡的梯度下降法 ,和爬山演算法做的 事情幾乎一樣 ,只是方向永遠是 梯度方向而已
這些方法 ,不管是在 1 維、 2 維、 3 維、 4 維 還是更高維空間,都是管用的
但是 ,通常只能找到《區域最高點或最 低點》,無法保證找到全域最高 點或最低點。
在上面的例子中 ,圖形最後都對應到了《函數》 ,而函數畫出來的圖形,讓我們對 結果有了視覺化的感受 …
而且不只如此 ,函數還可以用來轉換圖形
像是計算機圖學裏的 ,《縮放、旋轉》等變換都可以用矩陣函數表示
如果把矩陣加大一維 ,那麼就可以納入《平移》變換
平移、縮放、旋轉三種運算 ,形成的變換屬於仿射變換 (affine transformation) ,因此是仿射幾何學的特例 …
仿射變換 ,是碎形幾何的基礎
如果把旋轉運算放到三維空間 ,就可以得到針對不同軸心的三種旋轉運算 對 x 軸旋轉 對 y 軸旋轉 對 z 軸旋轉
於是圖形的呈現問題 ,就成了《矩陣運算》的問題
但是 ,由於我們的顯示器通常是二維的 ,要把三維物體顯示在二維平面中 那該怎麼辦呢?
透視投影可以解決這個問題
西洋文藝復興時期 單點透視法也成了繪畫的一大特色 中國的繪畫就沒有經過這樣的時期 ( 水墨畫完全不管比例問題 )
所以 ,笛卡兒的《解析幾何》對程式人 而言,可以說是一種《常識》
因為寫程式常常用到 ,但程式人卻不太知道自己正在 使用《幾何學知識》 …
以座標代表《點》 ,然後以《函數或方程式》代表《線》的 方式,早已深深地烙印在程式人的腦海 裡,不需要特別強調背後的數學了 …
空間
在數學上、所謂的空間,是一個加上了某些《數學結構》的集合。
正定 (Positive Definite)
在數學上
正定函數
正定函數的定義如下:
- d(x, y) ≥ 0 (非負性,或稱分離公理)
- d(x, y) = 0 若且唯若 x = y (同時公理)
正定矩陣
一個 n×n 的實對稱矩陣 M是正定的,若且唯若對於所有的非零實係數向量 z,都有 $z^T M z>0$ 。
範數
向量空間中的《範數》(Norm),是一個具有下列特性的函數。
- $
p(v) \ge 0$(半正定性) - $
p(a v) = |a| p(v)$(絶對一次齊次性) - $
p(u + v) \le p(u) + p(v)$ ([[三角不等式]]) - $
p(v)=0$ ,若且唯若 v 是《零向量》([[正定性]])
假如拿掉第 4 條,那麼該範數稱為《半範數》(Seminorm)。
度量空間
最常見的一種空間是《度量空間》 (Metric Space) ,《度量空間》是《集合》加上了《距離函數》的結果。
集合 X 上的度量 (Metric) 為一函數 (稱之為「距離函數」或簡稱為「距離」)
d : X × X → R
這裡的 R 是實數的集合,且對於所有 X 內的 x、y、z,均滿足如下條件:
- d(x,y) 為正定函數。
- d(x, y) = d(y, x) (對稱性)
- d(x, z) ≤ d(x, y) + d(y, z) (次加性 / 三角不等式)。
條件 1 與條件 2 為《正定函數》的定義。
最常見的度量空間是《歐氏空間》,其《距離度量》如下:
$d(x,y):=\sqrt{(x_1-y_1)^2 +(x_2-y_2)^2 + \cdots +(x_n-y_n)^2} = \sqrt{\sum_{i=1}^n(x_i-y_i)^2}$
在《向量空間》中,上述的《歐幾里得距離度量》,稱為《歐幾里得範數》。
點變換與矩陣
矩陣轉換是計算機圖學的核心觀念,當您用 3D 建模軟體時,會不斷使用《平移、縮放、旋轉》等動作,而這些動作都牽涉到大量的《矩陣運算》,所以《繪圖卡和GPU》裏都會透過加入很多 ALU 進行平行運算,以便加速這些矩陣的運算過程。
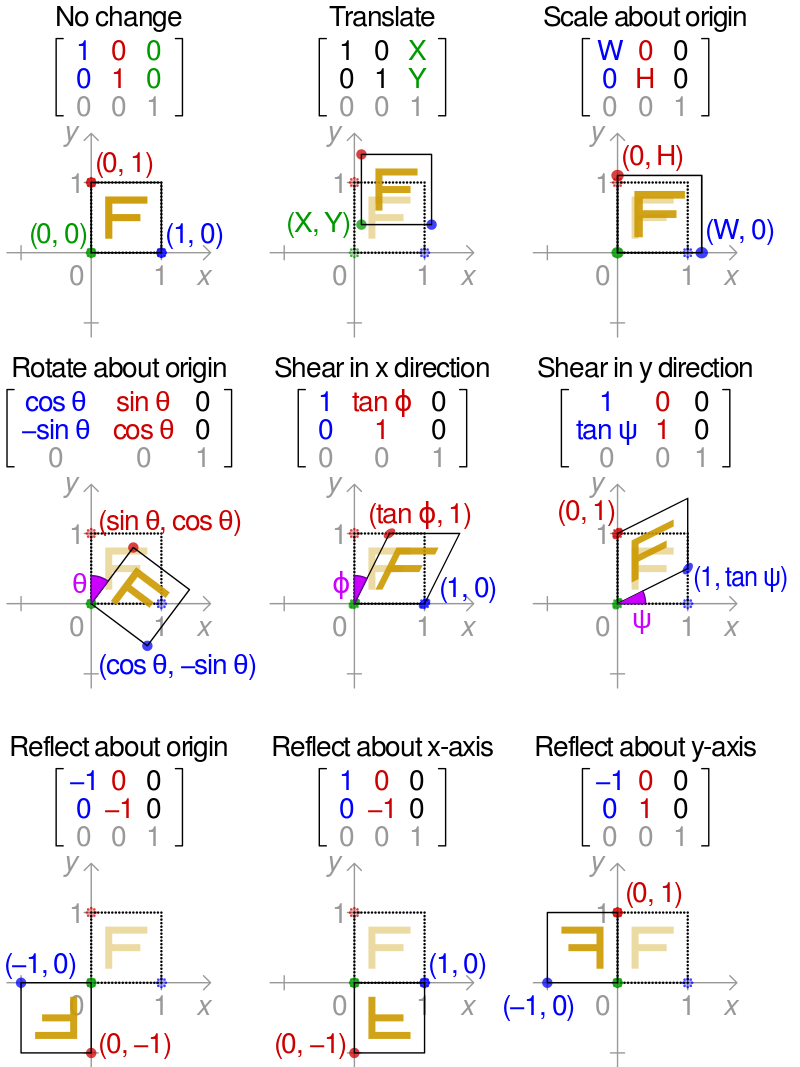
二維的轉換矩陣之效果