F5-物理之中的數學波動
力、向量與內積
物理學中最重要的觀念是《力》,在牛頓力學中是如此,電磁學中也是如此,到了相對論與量子力學,也是如此。
數學中使用《向量》(Vector) 表達力的觀念,用來描述力的方向和大小。
{\vec {a}}=[a_{1},a_{2},\cdots ,a_{n}]
對於那些瀰漫整個空間中的《力》,我們會用《場》(Field) 來表達。
向量之間可以做《內積》和《外積》等運算,其中的內積運算如下:
\vec{a}\cdot \vec{b} = \sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n
以上的內積定義是在《歐式空間》底下的定義,如果擴充到複數上,內積可以定義如下:
\langle x, y \rangle = \sum_{k=1}^n \overline{x_k} y_k
假如我們將向量推廣到《可數無限維》,甚至是《不可數無限維》,那麼是否還有內積呢?
答案是可以的!
內積空間
在數學上,《希爾伯特空間》定義為《完備的內積空間》,上述的《具有內積運算的歐式空間》,是《希爾伯特空間》的一個範例。
更一般的希爾伯特空間都是無窮維的,假設 B 是一個《可數無限集合》,可以定義其上的 $l^2$ 序列空間如下:
\ell^2(B) =\left\{ x:B \rightarrow \mathbb{C}\,\bigg|\,\sum_{b \in B} \left|x \left(b\right)\right|^2 < \infty \right\}
此空間在定義如下內積後,成為一個完備的內積空間 (希爾伯特空間):
\langle x, y \rangle = \sum_{b \in B} \overline{x(b)} y(b)
函數空間
如果將《可數無限維》繼續擴展到《不可數無限維》的《函數空間》上,就會出現《 $L^2(X)$ 勒貝格空間》,其中的內積定義如下:
\langle f,g\rangle=\int_X \overline{f(t)} g(t) \ d \mu(t)
那麼函數之間有了內積,也就會有《正交性》的概念出現了,只要兩個函數的內積為 0,那麼我們就說這兩個函數正交。
當《歐氏空間》中兩個向量 a, b 垂直 (正交) 的時候,其內積為 0 ,那麼在勒貝格空間中,哪些函數會互相正交呢?
三角函數的正交性
這個問題的解答有很多,但若我們將焦點放在 sin(nx) , cos (nx) 這類型的函數上,會發現這些不同的三角函數的內積都為零,所以這類函數兩兩互相正交 (除了和自己不正交以外)。
也就是說, cos(nx) 和 cos(mx) 只要 m, n 都是整數且不相等的情況下,其內積為零。
\int_{-\pi}^{\pi} \cos(mx)\, \cos(nx)\, dx = 0, \quad m, n \ge 1, m \ne n\,
同樣的 sin(nx) 和 sin(mx) 之間也是如此:
\int_{-\pi}^{\pi} \sin(mx)\, \sin(nx)\, dx = 0, \quad m, n \ge 1, m \ne n\,
而且 sin(nx) 和 cos(mx) 則必定相垂直 (內積為零)。
\int_{-\pi}^{\pi} \cos(mx)\, \sin(nx)\, dx = 0, \quad m, n \ge 1,
函數空間的正交分解
在歐氏空間中,n 維向量可以透過正交坐標系,分解成 n 個座標值。
同樣的,在 《勒貝格空間》這樣的《不可數無限維函數空間》上,一個函數也可以被 sin(nx) cos(mx) 這類的正交體系,分解成《無限多個座標值》,這些座標值就是其係數。
然後我們只要將函數 f 投影到 sin(nx), cos(mx) 上,就可以得到這些座標值。
\begin{aligned}
a_{n}&={\frac {1}{\pi}}\int_{-\pi}^{\pi} f(x)\cdot \cos(nx)\ dx \\
b_{n}&={\frac {1}{\pi}}\int_{-\pi}^{\pi} f(x)\cdot \sin(nx)\ dx
\end{aligned}
如果將範圍縮放到 L 並以 x0 為起點的話,就會變成如下形式:
\begin{aligned}
a_{n}&={\frac {2}{L}}\int _{{x_{0}}}^{{x_{0}+L}}f(x)\cdot \cos({\tfrac {2\pi nx}{L}})\ dx
\\
b_{n}&={\frac {2}{L}}\int _{{x_{0}}}^{{x_{0}+L}}f(x)\cdot \sin({\tfrac {2\pi nx}{L}})\ dx
\end{aligned}
透過尤拉公式 $e^{ix} = \cos x + i\sin x$ 我們可以進一步將以上兩算式整併成一式:
c_{n}={\frac {1}{L}}\int _{{x_{0}}}^{{x_{0}+L}}f(x)\cdot e^{{-i{\tfrac {2\pi nx}{L}}}}\ dx
更視覺化的來看,將函數 f(x) 分解成 sin(nx), cos(mx) 的過程,基本上就是各種頻率圓周運動的疊加過程。
鋸齒波的分解疊加方法如下:
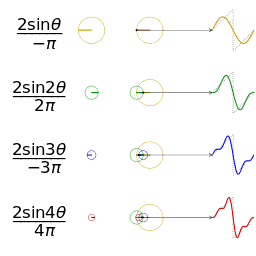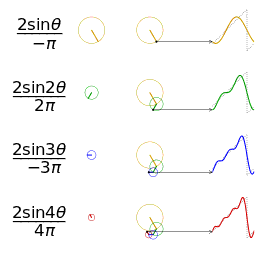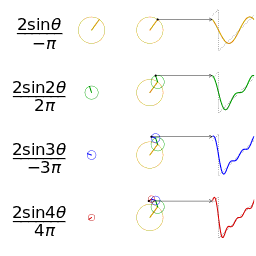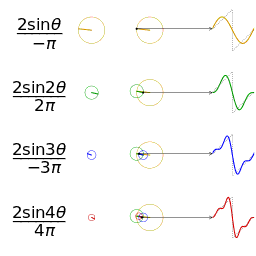
方波的分解疊加方法如下:
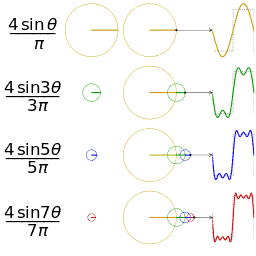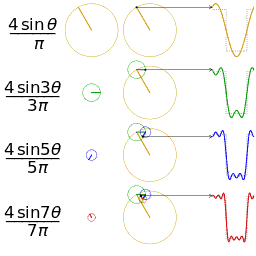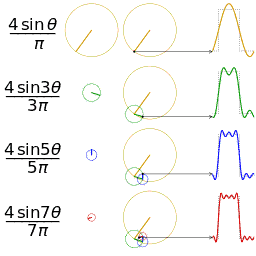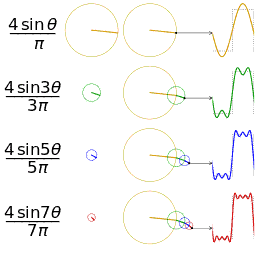
波函數的微分方程
如果改用微分方程去描述一個波函數,那麼通常會是二次的微分方程,這是因為 sin(x), cos(x) 等函數,都具有《二次微分後會變成自己常數倍》的特性。
舉例而言,對於 sin(x) 而言:
\begin{aligned}
\sin'(x) &= \cos(x) \\
\sin''(x) &= \cos'(x) = -\sin(x)
\end{aligned}
所以 sin(x) 是下列微分方程的一個解: (同理,cos(x) 也是)
f''(x) = -f(x)
對於 sin(nx) 而言,有下列微分關係:
\begin{aligned}
\sin'(nx) &= n \cos(nx) \\
\sin''(nx) &= n \cos'(nx) = -n^2 \sin(x) \\
\end{aligned}
所以 sin(nx) 是下列微分方程的一個解: (同理,cos(nx) 也是)
f''(x) = -n^2 f(x)
所以當我們看到二次微分方程式的時候,就會直接聯想其解可能是《波函數》。
像是馬克士威的電磁波方程式:
\begin{aligned}
& \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right){\mathbf {E}}\ =\ 0
\\
& \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right){\mathbf {B}}\ =\ 0
\end{aligned}
量子力學的薛丁格波動方程: (無場勢自由粒子版本)
{\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)=i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)} ;
等等方程式,都是二次的微分方程式,因此其解都是由 sin(nx) , cos(mx) 組成的波動函數。
這就是物理當中的數學波動函數!