陳鍾誠

Version 1.0

傅立葉轉換

Python 程式

# https://docs.scipy.org/doc/numpy/reference/generated/numpy.fft.fft.html
import numpy as np
import matplotlib.pyplot as plt
t = np.arange(256)
sp = np.fft.fft(np.sin(t))
freq = np.fft.fftfreq(t.shape[-1])
plt.plot(freq, sp.real, freq, sp.imag)
plt.show()

執行

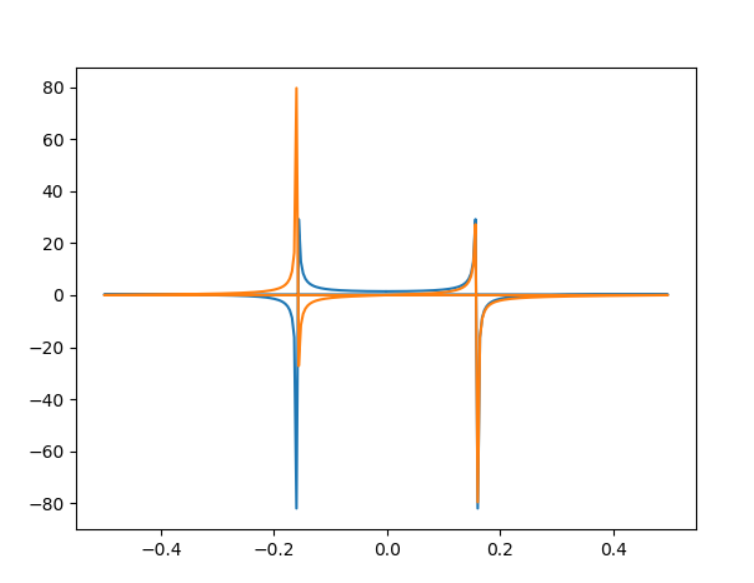
# https://stackoverflow.com/questions/25735153/plotting-a-fast-fourier-transform-in-python

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack

# Number of samplepoints
N = 600
# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = scipy.fftpack.fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), int(N/2))

fig, ax = plt.subplots()
ax.plot(xf, 2.0/N * np.abs(yf[:N//2]))
plt.show()

執行結果

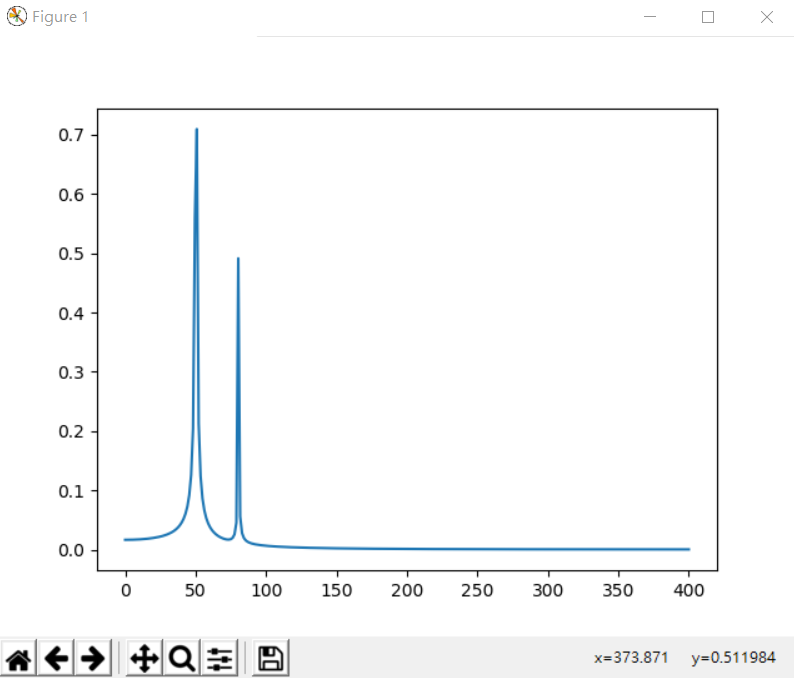
一維傅立葉變換換

\hat{f}(\xi) = \int_{-\infty}^\infty f(x)\ e^{- 2\pi i x \xi}\,dx

f(x) = \int_{-\infty}^\infty \hat f(\xi)\ e^{2 \pi i \xi x}\,d\xi

理論: 傅立葉轉換在影像處理中的用途

參考

$f(x) = e^{i x} $ 的泰勒級數

傅立葉轉換其實就是一種泰勒級數，是自然對數 e (或稱尤拉數) 的虛數次方 $e^{i x} $ 的泰勒級數，天啊! 又自然對數又虛數，怎麼這麼抽象 ! 這就是數學厲害的地方，實數成立後就想辦法證明看看虛數可不可以用，深入探討後就發現微分函數中的自然對數的虛數次方更好用，以下我們就將來探討這個神奇的函數。

若我們將 [[[ca:tylor | 泰勒展開式與函數逼近論]] 中公式 (7) 中的 f(x) 代換成 $e^{ix} $，則將會得到下列函數：

e^{i x} = 1 + i \frac{x}{1!} - \frac{x^2}{2!} - i \frac{x^3}{3!} + ...

天啊、所有的 $f^k $ 通通都不見了，只剩奇數次方中的負號與 i 還存在，好簡潔的公式。

更神奇的是、若我們將 sin(x) 與 cos(x) 的泰勒級數寫出來，就會發現下列泰勒展開式：

cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + ... 

sin(x) = \frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} + ...

根據 ([9]) ([10]) ([11]) 三個算式仔細比較，我們可以發現下列驚人的事實：

e^{i x} = cos(x) + i * sin(x)

這樣的結果令人驚訝的原因是，原本不相關的東西竟然透過泰勒級數連結起來了，數學果真厲害。

以三角函數逼近一般函數 f(x)

假設我們希望用三角函數 sin(nx) 與 cos(nx) 逼近一個函數 f(x)，我們可以將這個式子寫成如下算式：

f(x) = \sum^{\infty}_{n=0} a_n cos(n x)+ b_n sin(n x)

由於算式 ([12]) 我們可將三角函數轉為自然指數如下：

cos(n x) + i * sin(n x) = e^{i n x}

因此、若我們允許系數 $b_n $ 包含虛數，則我們可將算式 ([13]) 寫成如下的自然指數。

f(x) = \sum^{\infty}_{n=0} F_n e^{i n x}

算式 ([15]) 就稱為傅立葉級數，也就是利用 sin(nx) 與 cos(nx) 逼近函數的一種方法。

再根據類似推導 [[[ma:taylor | 泰勒展開式與函數逼近論]] 中算式 (5) 泰勒展開式的方法，我們可以導出傅立葉級數的係數如下：

F_t = \frac{1}{2\pi} \int^{\pi}_{-\pi} f(x) e^{i t x} dx

若是在不連續的狀況之下，上述公式要改寫成總和式如下：

F_n = \frac{1}{N} \sum^{N-1}_{k=0} f(k) e^{\frac{- i k 2 \pi n}{N}}

這個係數 Fn 的計算方法，就稱為傅立葉轉換，其中 Fn 與 an, bn 的關係如下：

x0xnx-n
$F_0 = \frac{1}{2}$$F_n= \frac{1}{2} (a_n- i b_n)$$F_{- n}= \frac{1}{2} (a_n+i b_n)$
$a_0 = 2 c_0$$a_n=F_n+F_{- n}$$ b_n=i (F_n-F_{-n})$

到目前為止，我們已經將傅立葉轉換之所以可以用來逼近函數的數學公式說明清楚了，傅立葉轉換就是用來逼近 f(x) 函數的 sin(nx), cos(nx) 項的係數，因此、只要算出這些係數，就可以重新組合出 f(x)。

以下圖形代表以傅立葉級數進行逼近時頻率為 0, 1, 2, …,n, 之情況 ：

以下圖形代表利用 sin(nx) 的波形去組合出函數 f(x) 的一個情況，其中：

上圖中：

紅色線代表 $c_1 sin(1 x) $ 黃色線代表 $c_1 sin(1x)+c_2 sin(2x) $ 綠色線代表 $c_1 sin(1x)+c_2 sin(2x)+c_3 sin(3x) $ 藍色線代表 $c_1 sin(1x)+c_2 sin(2x)+c_3 sin(3x)+c_4 sin(4x) $ 紫色線代表 $c_1 sin(1x)+c_2 sin(2x)+c_3 sin(3x)+c_4 sin(4x)+c_5 sin(5x) $

根據這種方法、前面的項數加得越多，逼近的程度就越高、越精確。

而 sin(nx) , cos(nx) 的特性，就是在 n 愈小時越平滑，這些平滑的函數可以用來表示圖形中變化較小的部份，當 n 越大時，變化越快且頻率越高，因此、 n 大的部分代表了影像快速的細微變化，這些細微變化常是人眼的視覺所自動忽略的，因此、可以將高頻的部分省掉，留下低頻的部份，影像看起來仍然會非常接近原來的影像，這就是電腦進行影像壓縮所用的方法。

另外、若要從以轉換後的係數 Fn 再轉回原來的 an, bn, 則可進行下列反向計算，這個逆向計算方法就稱為逆向傅立葉轉換：

連續的狀況：

f(t) = \int^\infty_{- \infty} F(x) e^{i 2 \pi x t} dt

不連續 (離散) 的狀況：

f(n) = \sum^{N-1}_{k=0} F(k) e^{i 2 \pi k} \frac{n}{N}

結語

本文中我們介紹了如何利用多項式的不斷微分法導出泰勒級數，接著列出 $e^{i x} $ 函數的微分，並與 cos(x) + i*sin(x) 比較以導出傅立葉級數，然後利用傅立葉級數對影像進行轉換，而得到一個基於 cos 與 sin 的係數組，這個係數組所代表的乃是利用 sin, cos 的波形對影像進行逼近的結果，因而、當我們從中取出低頻率係數而捨棄高頻率係數時，就得到了一個非常近似於原始影像，但節省許多儲存空間的表示法，這幾乎就是所有影像壓縮技術的基礎。

JPEG 就是用 cosine transform 做的，也就是取傅立葉轉換中的 a0, …, an 的部份。

壓縮率這麼好的原因是：在頻率域其實是儲存某頻率波的係數，低頻部份通常很重要 (例如最低頻的常數其實就是整個色塊的平均值)，因此編碼時只要留下低頻部份 (a0, a1, …, ak)，高頻部份 (ak+1, … , an) 通常可以去除或減少取樣位元數，如此就達到了壓縮的目的。

參考程式


 Edit on GitHub