第 2 章 - 爬山演算法 Hill-Climbing
爬山演算法 (Hill Climbing) 是一種最簡單的優化算法,該方法就像模擬人類爬山時的行為而設計的,因此稱為爬山演算法。
程式究竟要怎麼爬山呢?且讓我們用一張圖來看看。
假如我們在 Google 裏輸入一個算式,Google 會幫我們畫出該函數。舉例而言,如果我在 Google 輸入 x^2+3x+5 這個算式,您會看到下列圖形:
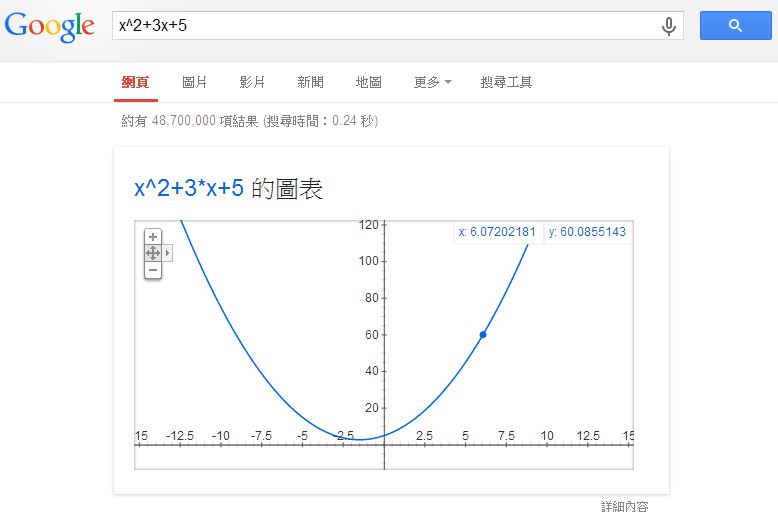
這時您可以移動滑鼠,圖形會出現一個可移動的小藍點,該點會沿著曲線移動,上圖中 (x, y) 座標顯示為 x:6.07202181, y:60.0855143, 就是那個小藍點所在的位置。
如果我們想要寫程式尋找這個函數的最低點,那我們應該怎麼找呢?
其實方法很簡單,就是一直往低的地方走,一直走到最低點,然後你會看到左右兩邊都沒辦法更低了,於是就停止尋找,傳回該最低點作為答案。
這個方法,就像是水往低處流一樣,不斷的往更低的方向流,最後一定會流到一個山谷,然後就積成一個湖了。
但是、既然這樣,那為甚麼叫做爬山演算法,而不叫「流水下山演算法」呢?
其實、只要反過來看就行了,如果我們想要找的是最高點,而不是最低點,那整個行為就會像爬山一樣,只是最後爬到山頂就會停了。
採用這種想法,若我們想找 $x^2+3x+5$ 這個函數的最高,我們可以在 Google 輸入 -(x^2+3x+5) 就可以看到那座山了,以下是 Google 顯示的結果:
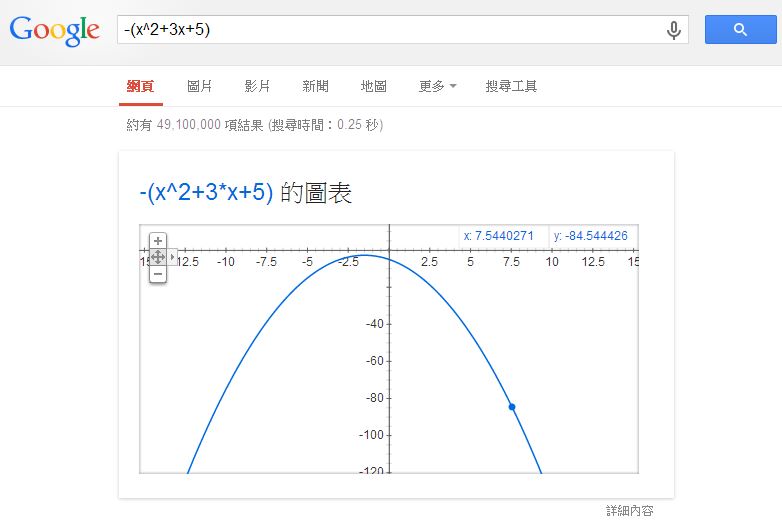
當然、如果函數有很多山峰,那這種方法只能走到小山丘就會停了。這時您可能會說,那為甚麼不再繼續往更高的山走去呢?
關於這點,並不是不行,只是程式沒有眼睛,也沒辦法一眼望去把所有的地形都給看光,然後知道更高的山峰在哪裡?
如果我們用上面水往低處流的想法,您就會清楚爬山演算法所遭遇的困難了。當您像水一樣往下流,到了谷底之後,由於四周都是山壁,所以您根本看不到更低的谷到底在哪裡,所以只好就停下來了。
此時、除非你爬出山谷,否則根本不可能找到更深的谷,這就是「流水下山演算法」所遭遇到的困難了。以下是我們用 Google 顯示 (x-5)*(x-3)*(2x+5)*(x+3) 這個具有兩個山谷的函數,所得到的圖形。
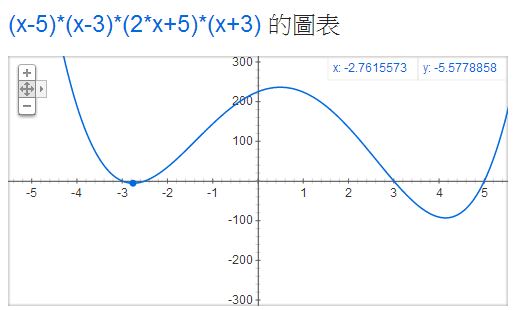
假如我們在上圖中左邊的山谷,那麼怎麼能知道右邊還有一個更低的山谷呢?這就是「流水下山演算法」的困難之所在了!
當然、也有人試圖提出一些企圖找到更深的谷,或爬到更高的山的演算法,這些演算法往往是以爬山演算法為基礎,然後再作一些改良,像是「模擬退火演算法」(Simulated Annealing Algorithm) 或大洪水演算法 (Great Deluge algorithm) 等等,這些方法都是企圖讓「流水下山演算法」有機會跳出山谷而設計的方法。
當然、您也可以企圖加上「衝力」之類的想法讓「流水下山演算法」可以衝出低谷,但是到底要衝多久,還有該往哪個方向衝才對呢?那這種方法是否該改叫「衝山演算法」呢?
當然、我是沒有聽過這種名稱啦!
另外、對於上述的單變數函數而言,不是往左邊走就是往右邊走,但是如果有兩個變數,例如像 x^2+y^2+3x+5y+6 ,但是只有一個山谷,那麼我們該修改哪個變數呢?舉例而言,以下就是 Google 所畫出的 x^2+y^2+3x+5y+6 之圖形。
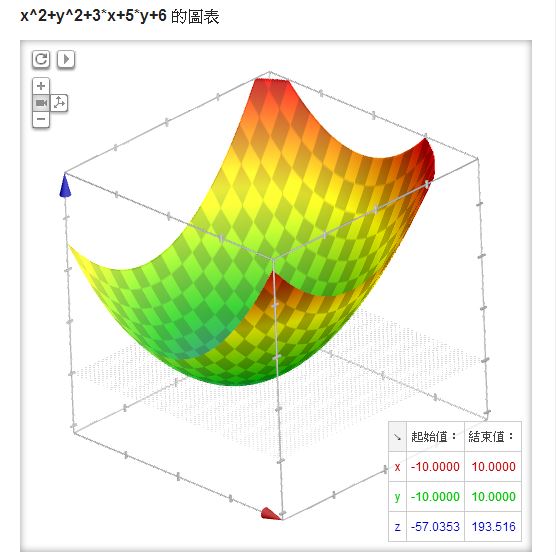
在上述的雙變數情形中,我們可以隨機的挑一個變數,然後向左或向右移動一小步,只要移動後的點更低就接受,如果連續很多次移動都沒辦法找到更低的點,就認為已經到達山谷,這樣的方法其實還蠻有效的,這種方法可以稱為「隨機下山演算法」 (反過來英文中以爬山的角度來看,所以稱為隨機爬山演算法 Stochastic Hill Climbing Algorithm)。
當然、隨機的方法有時會比較沒效率,如果我們可以很容易的透過微積分計算斜率 (導數) 的話,那麼不管幾個變數,我們都可以計算出山坡上最陡峭的那一個方向,這種微積分概念稱為「梯度」,而這也是我們下一章要討論的內容。
實作:以爬山演算法尋找函數最高點
簡介
以下是「爬山演算法」 (Hill-Climbing Algorithm) 的一個簡易版本,其方法超簡單,就是一直看旁邊有沒有更好的解,如果有就移過去。然後反覆的作這樣的動作,直到旁邊的解都比現在的更差時,程式就停止,然後將那個位於山頂的解傳回,就完成了。
Algorithm HillClimbing(f, x)
x = 隨意設定一個解。
while (x 有鄰居 x' 比 x 更高)
x = x';
end
return x;
end
當然、這種演算法只能找到「局部最佳解」(local optimal),當整個空間有很多山頂的時候,這種方法會爬到其中一個山頂就停了,並不一定會爬到最高的山頂。
程式碼
檔案: HillClimbingSimple.js
var util = require("util");
var log = console.log;
function f(x) { return -1*(x*x+3*x+5); }
// function f(x) { return -1*Math.abs(x*x-4); }
var dx = 0.01;
function hillClimbing(f, x) {
while (true) {
log("f(%s)=%s", x.toFixed(4), f(x).toFixed(4));
if (f(x+dx) >= f(x))
x = x+dx;
else if (f(x-dx) >= f(x))
x = x-dx;
else
break;
}
}
hillClimbing(f, 0.0);
執行結果
求解 : $-(x^2+3x+5)$ 的最高點,也就是 $x^2+3x+5$ 的最低點。
D:\Dropbox\Public\web\ai\code\optimize>node hillClimbingSimple
f(0.0000)=-5.0000
f(-0.0100)=-4.9701
f(-0.0200)=-4.9404
f(-0.0300)=-4.9109
f(-0.0400)=-4.8816
f(-0.0500)=-4.8525
...
f(-1.4500)=-2.7525
f(-1.4600)=-2.7516
f(-1.4700)=-2.7509
f(-1.4800)=-2.7504
f(-1.4900)=-2.7501
f(-1.5000)=-2.7500
如果我們將上述程式的 f(x) 換成註解中的那個,也就是將 f(x) 換成如下版本:
function f(x) { return -1*Math.abs(x*x-4); }
那麼就可以用來求解 $|x^2-4|$ 的最低點,也就是尋找 4 的平方根,以下是執行結果:
D:\Dropbox\Public\web\ai\code\optimize>node hillClimbingSimple
f(0.0000)=-4.0000
f(0.0100)=-3.9999
f(0.0200)=-3.9996
f(0.0300)=-3.9991
f(0.0400)=-3.9984
f(0.0500)=-3.9975
...
f(1.9500)=-0.1975
f(1.9600)=-0.1584
f(1.9700)=-0.1191
f(1.9800)=-0.0796
f(1.9900)=-0.0399
f(2.0000)=-0.0000
您可以看到上述程式正確的找到 4 的平方根是 2,而我們所用的方法與求解 $-(x^2+3x+5)$ 的最高點幾乎是一模一樣的,只是把函數換掉而已。
結語
您可以看到上述用爬山演算法尋找函數最高點或最低點的程式,其實非常的簡單,只不過是看看兩邊是否有更好的解,如果有就移過去罷了。
但是、這麼簡單的演算法,其實威力是非常強大的,這種方法可以求解的問題非常的多,很多人工智慧上非常重要的問題,其實都只不過是在進行函數優化的動作,也就是尋找某個函數的低點或高點而已,這些問題其實大部分都可以使用爬山演算法來求解。
當然、要能尋找更複雜函數的「區域最佳解」,還必須進一步的對上述程式進行封裝與抽象化,我們將在下一篇文章中解說將上述爬山程式抽象化後的版本,並用該程式來求更複雜函數的解。