圖形演算法 Graph Algorithm
簡介
在離散數學、演算法與人工智慧的領域,很多問題可以表示為「節點與連線所形成的圖形」,一個程式要解決某問題其實是在這個圖形裏把目標節點給找出來,於是問題求解就簡化成了圖形的搜尋,我們只要把解答給「找出來」就行了。
圖形搜尋的方法大致可以分為「深度優先搜尋 (Depth-First Search, DFS)、廣度優先搜尋 (Breath-First Search, BFS)、最佳優先搜尋 (Best-First Search, BestFS) 等三類。
然後針對最佳優先搜尋的部份,還有一種具有理論背景,且較為強大好用的 A* 搜尋法可採用。
圖形的表達
圖形是由節點 (node) 與連線 (edge) 所組成的。舉例而言,以下是一個包含六個節點與十條連線的簡單圖形。
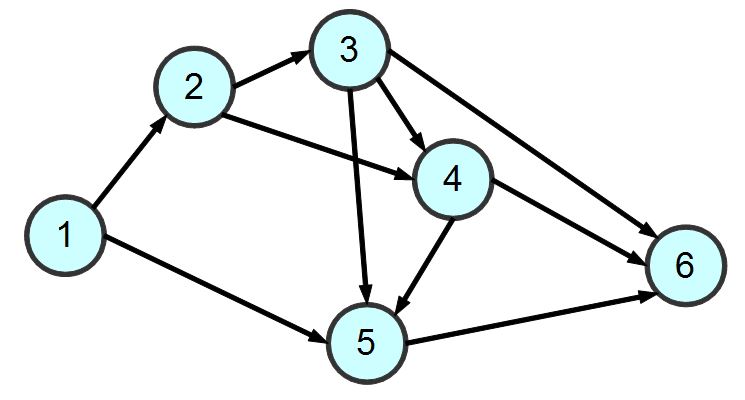
我們可以使用下列《資料結構》表達圖形:
當然也可以《因語言制宜》,採用最適合該語言的資料結構。
在 javascript 中,我們可以採用下列類似相鄰串列的方式表達圖形。
var g = { // graph: 被搜尋的網路
1: {n:[2,5], v:0}, // n: neighbor (鄰居), v: visited (是否被訪問過)
2: {n:[3,4], v:0},
3: {n:[4,5,6], v:0},
4: {n:[5,6], v:0},
5: {n:[6], v:0},
6: {n:[], v:0}
}
深度優先搜尋
所謂的「深度優先搜尋」 (Depth-First Search, DFS),就是一直往尚未訪問過的第一個鄰居節點走去的一種方法,這種方法可以採用程式設計中的「遞迴技巧」完成,以下是深度搜尋的演算法:
Algorithm DFS(graph, node) { // 深度優先搜尋,graph : 圖形, node:節點
if (node.visited) return; // 如果已訪問過,就不再訪問
node.visited = 1; // 並設定為已訪問
foreach (neighbor of node) // 對於每個鄰居
DFS(graph, neighbor); // 逐一進行深度優先搜尋的訪問。
end
您可以看到上述的演算法中,我們單純採用遞迴的方式,就可以輕易的完成整個 DFS 演算法。
當然、實作為程式的時候,會稍微複雜一點,以下是使用 Javascript 的實作方式:
function dfs(g, node) { // 深度優先搜尋
if (g[node].v !=0) return; // 如果已訪問過,就不再訪問
printf("%d=>", node); // 否則、印出節點
g[node].v = 1; // 並設定為已訪問
var neighbors = g[node].n; // 取出鄰居節點
for (var i in neighbors) { // 對於每個鄰居
dfs(g, neighbors[i]); // 逐一進行訪問
}
}
針對上述的範例圖形,若採用深度優先搜尋,其結果可能如下所示 (圖中紅色的數字代表訪問順序)
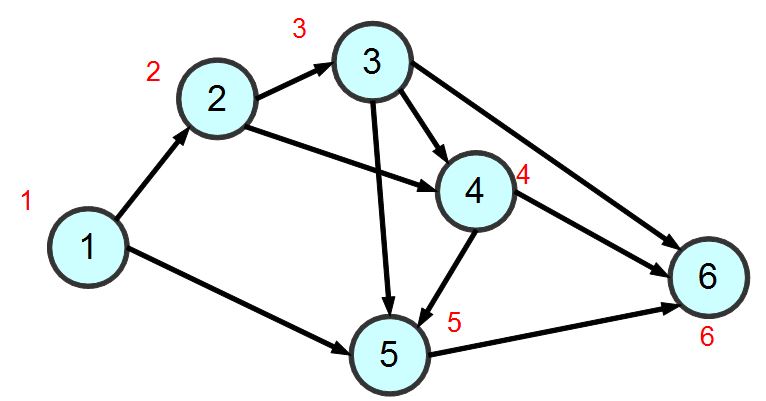
廣度優先搜尋
雖然深度優先搜尋可以搜尋整個圖形,但是卻很可能繞了很久才找到目標,於是從起點到目標可能會花費很久的時間 (或說路徑長度過長)。
如果我們想找出到達目標最少的步驟,那麼就可以採用「廣度優先搜尋」 (Breath-First Search, BFS) 的方式。
廣度優先搜尋 BFS 是從一個節點開始,將每個鄰居節點都一層一層的拜訪下去,深度最淺的節點會優先被拜訪的方式。
舉例而言,針對上述的圖形範例,若採用「廣度優先搜尋 BFS 」的方式,那麼拜訪順序將會如下所示:
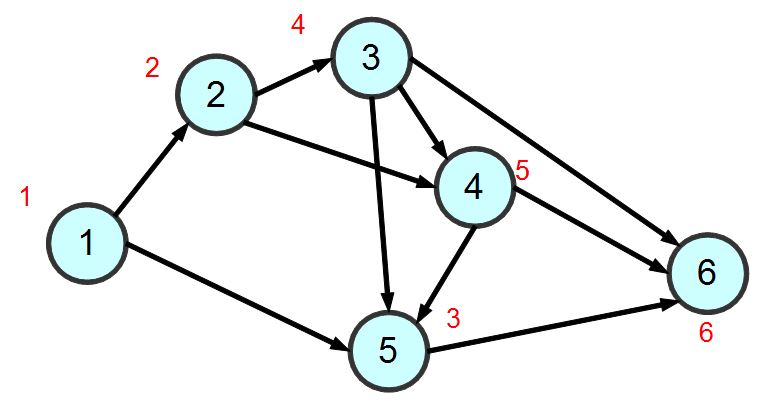
要能用程式進行廣度優先搜尋,必須採用「先進先出」(First-in First-Out, FIFO) 的方式管理節點,因此通常在「廣度優先搜尋」裏會有個佇列 (queue) 結構,以下是 BFS 的演算法:
Algorithm BFS(graph, queue)
if queue.empty() return;
node = queue.dequeue();
if (!node.visited)
node.visited = true
else
return;
foreach (neighbor of node)
if (!neighbor.visited)
queue.push(neighbor)
end
以下是使用 Javascript 的 BFS 程式實作片段:
function bfs(g, q) { // 廣度優先搜尋
if (q.length == 0) return; // 如果 queue 已空,則返回。
var node = dequeue(q); // 否則、取出 queue 的第一個節點。
if (g[node].v == 0) // 如果該節點尚未拜訪過。
g[node].v = 1; // 標示為已拜訪
else // 否則 (已訪問過)
return; // 不繼續搜尋,直接返回。
printf("%d=>", node); // 印出節點
var neighbors = g[node].n; // 取出鄰居。
for (var i in neighbors) { // 對於每個鄰居
var n = neighbors[i];
if (!g[n].visited) // 假如該鄰居還沒被拜訪過
q.push(n); // 就放入 queue 中
}
bfs(g, q);
}
最佳優先搜尋
但是、上述兩個方法其實都還不夠好,深度搜尋會猛衝亂衝,而廣度搜尋則會耗費太多的記憶體,並且沒有效率,無法很快的找到目標點。
假如我們能夠知道哪些點距離目標點最近,也就是哪些點比較好的話,那就能採用「最佳優先搜尋 (Best-First Search) 的方式來搜尋了。
最佳優先搜尋的實作方法與廣度優先搜尋類似,但是並不採用佇列 (queue) ,而是採用一種根據優先程度排序的結構,每次都取出最好的那個繼續進行搜尋。
但是、節點的好壞通常很難評估,單純採用某種距離去評估往往會過度簡化問題,這點往往是最佳優先搜尋的困難之所在。
還好、有時我們不需要非常精確的評估,只要問題符合 $$h(x) \leq d(x,y)+h(y)$$ 這樣的單調 (monotone) 特性,就可以使用 A* 演算法來進行較快速的搜尋,這種方法比廣度優先搜尋通常快很多,因為 A* 不會搜尋所有節點,而是有系統的朝著整體較好的方向前進,這種方法在電腦遊戲 (Game) 上常被用在 NPC (非人類角色) 的智慧型搜尋行為設計上面,是人工智慧搜尋方法中較強大的一種。
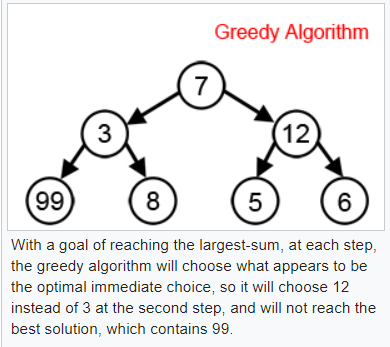
貪婪圖形搜尋
對於 Graph 類的結構,我們也可以用『貪婪算法』來處理,每次都向下一層中最好的分支走去。
最小擴展樹
檔案: minimalSpanningTree.js
// https://gist.github.com/n8agrin/3629426
var _ = require('underscore');
var nodes = ["A", "B", "C", "D", "E", "F", "G"];
var edges = [
["A", "B", 7], ["A", "D", 5],
["B", "C", 8], ["B", "D", 9], ["B", "E", 7],
["C", "E", 5],
["D", "E", 15], ["D", "F", 6],
["E", "F", 8], ["E", "G", 9],
["F", "G", 11]
];
function kruskal(nodes, edges) {
var mst = [];
var forest = _.map(nodes, function(node) { return [node]; });
var sortedEdges = _.sortBy(edges, function(edge) { return -edge[2]; });
while(forest.length > 1) {
var edge = sortedEdges.pop();
var n1 = edge[0],
n2 = edge[1];
var t1 = _.filter(forest, function(tree) {
return _.include(tree, n1);
});
var t2 = _.filter(forest, function(tree) {
return _.include(tree, n2);
});
if (t1 != t2) {
forest = _.without(forest, t1[0], t2[0]);
forest.push(_.union(t1[0], t2[0]));
mst.push(edge);
}
}
return mst;
}
console.log(kruskal(nodes, edges));
執行結果:
$ node minimalSpannintTree.js
[ [ 'C', 'E', 5 ],
[ 'A', 'D', 5 ],
[ 'D', 'F', 6 ],
[ 'B', 'E', 7 ],
[ 'A', 'B', 7 ],
[ 'E', 'F', 8 ],
[ 'B', 'C', 8 ],
[ 'E', 'G', 9 ] ]
最短路徑算法
- 圖形中兩點間的最短路徑: Dijkstra 算法
- 所有點之間的最短路徑: Floyd Warshall 算法