貪婪演算法 Greedy Algorithm
『貪婪演算法』每次都會往目前看到最好的方向走去,而且盡量選取改善最多的那一步。
找零錢問題
舉例而言,若你買東西給了紙鈔,那麼能否寫一個程式自動計算應該『找多少零錢』,而且要盡量讓『找錢的銅板數量愈少愈好』?
這個問題可以用『貪婪算法』,從小於『剩餘金額』的最大類型銅板開始找起,因為這樣找一個零錢就可以『解決最多的剩餘金額』,所以是一種貪婪策略!
以下是這個問題的想法圖示!

貪婪爬山法
我們也可以用『貪婪算法』來完成『爬山演算法』的動作,原本爬山演算法只要看到更高就往那邊爬,但是貪婪算法則要往『斜率最大的方向爬』。
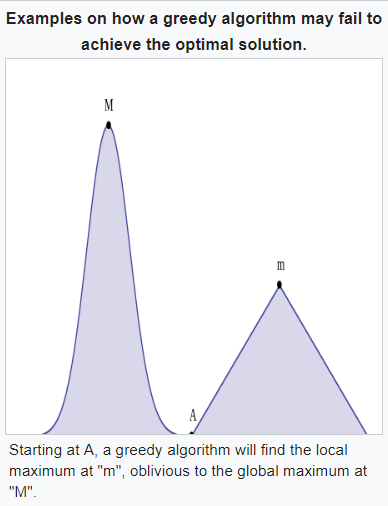
上圖是二維平面,看不太出『貪婪算法』與爬山演算法的差別,假如是『三維圖形』時,那麼『貪婪算法』就會變得和『梯度爬山法』一樣,總是朝著斜率最大的方向爬去。
霍夫曼編碼法
檔案: HuffmanCode.js
// 程式修改自 -- https://gist.github.com/1995eaton/86f10f4d0247b4e4e65e
// 參考 -- https://en.wikipedia.org/wiki/Binary_heap
/* 堆積:
插入節點: 在陣列的最末尾插入新節點。然後自下而上調整子節點與父節點(稱作 bubble-up 或 sift-up)
比較當前節點與父節點,不滿足「堆積性質」則交換。從而使得當前子樹滿足二元堆積的性質。
時間複雜度為 O(log n)。
刪除樹根:刪除時,把堆積儲存的最後那個節點移到填在根節點處。再從上而下調整父節點與它的子節點。
*/
class Heap { // 堆積結構 Heap
constructor (fn) {
this.fn = fn // fn 會取得排序欄位值
this.items = [] // items 為存放堆積的陣列
}
swap(i, j) {
let t = this.items[i]
this.items[i] = this.items[j]
this.items[j] = t
}
bubble(index) { // 冒泡調整,將大的往上調
var parent = ~~((index - 1) / 2)
if (this.item(parent) < this.item(index)) {
this.swap(index, parent)
this.bubble(parent)
}
}
item(index) {
return this.fn(this.items[index])
}
pop() {
return this.items.pop()
}
sift(index, end) {
var child = index * 2 + 1
if (child < end) {
if (child + 1 < end && this.item(child + 1) > this.item(child)) {
child++
}
if (this.item(index) < this.item(child)) {
this.swap(index, child)
return this.sift(child, end)
}
}
}
push() {
var lastIndex = this.items.length
for (var i = 0; i < arguments.length; i++) {
this.items.push(arguments[i])
this.bubble(lastIndex++)
}
}
length() {
return this.items.length
}
}
var Huffman = {
encode: function(data) {
var prob = {}
var tree = new Heap((e)=>e[0])
// 計算每個字出現的頻率
for (var i = 0; i < data.length; i++) {
if (prob.hasOwnProperty(data[i])) {
prob[data[i]]++
} else {
prob[data[i]] = 1
}
}
// 將整個陣列順序打亂,然後放進堆積中(節點:以 [出現次數, 字元] 的方式儲存。
Object.keys(prob).sort((a, b) => ~~(Math.random() * 2))
.forEach((e) => tree.push([prob[e], e]))
while (tree.length() > 1) { // 當還沒有全部形成一棵樹 (還有很多棵)的時候
var first = tree.pop(), second = tree.pop() // 取出頻率最小的兩個
tree.push([first[0] + second[0], [first[1], second[1]]]) // 將兩者合併成一個
}
// 上面迴圈完成後,樹已經建好了,開始進行編碼!
var dict = {}
var recurse = function(root, string) {
if (root.constructor === Array) {
recurse(root[0], string + '0') // 左邊為 0
recurse(root[1], string + '1') // 右邊為 1
} else {
dict[root] = string // 已經到樹葉節點,設定該字元的編碼。
}
}
tree.items = tree.pop()[1] // 取得樹根
recurse(tree.items, '') // 對樹上每個節點進行編碼
var result = ''
for (var i = 0; i < data.length; i++) {
result += dict[data.charAt(i)] // 對每個字元編碼後加入結果的 0101.... 字串
}
return {emap:dict, result:result}
},
decode: function(h) {
var data = h.result.split(''), dmap = {}
// 將 emap(ch)=>binary 反轉為 dmap(binary)=>ch
for (let ch in h.emap) {
let binary = h.emap[ch]
dmap[binary] = ch
}
var result = ''
while (data.length) {
var i = 0, cur = ''
while (data.length) {
cur += data.shift()
if (dmap.hasOwnProperty(cur)) { // 查查看這個長度的二進位是否在 dmap 中
result += dmap[cur] // 有的話就進行編碼
break
}
}
}
return result
}
}
var enc = Huffman.encode('TESTTESTTESTTESTTESTTESTTESTTEST123abc')
console.log('encode=', enc)
var dec = Huffman.decode(enc)
console.log('decode=', dec)
執行結果
$ node huffmanCode.js
encode= { emap:
{ '1': '10001',
'2': '1000001',
'3': '1000000',
T: '0',
a: '100001',
b: '10010',
c: '10011',
S: '101',
E: '11' },
result: '0111010011101001110100111010011101001110100111010011101010001100000110000001000011001010011' }
decode= TESTTESTTESTTESTTESTTESTTESTTEST123abc
結語
對於『找零錢,霍夫曼編碼法』,甚至是接下來圖論裏要講的《最小擴展樹》這類的問題而言,『貪婪算法』是可以找到最佳解的!
但是對於其他問題,每次都貪婪的走,並不見得能找到整體最好的結果,甚至有時候結果會很差,因此是否要用貪婪算法,得視問題而定。