分割擊破法 Divide & Conquer
二分搜尋法
如果你曾經學過《演算法》, 應該曾經使用過《二分搜尋法》
對於一個《連續函數》而言, 假如我們知道兩個點 (a,b) ,其值 f(a)>0 且 f(b)<0 ,這樣的話勢必有一個介於 (a,b) 之間的 c 值使得 f(c)=0, 假如我們每次都取 ,然後判斷要繼續搜 尋哪一半的話,這樣我們就得到了一個《二分搜 尋法》,可以較快速的找出 f(x)=0 的解答!
其想法圖示如下:
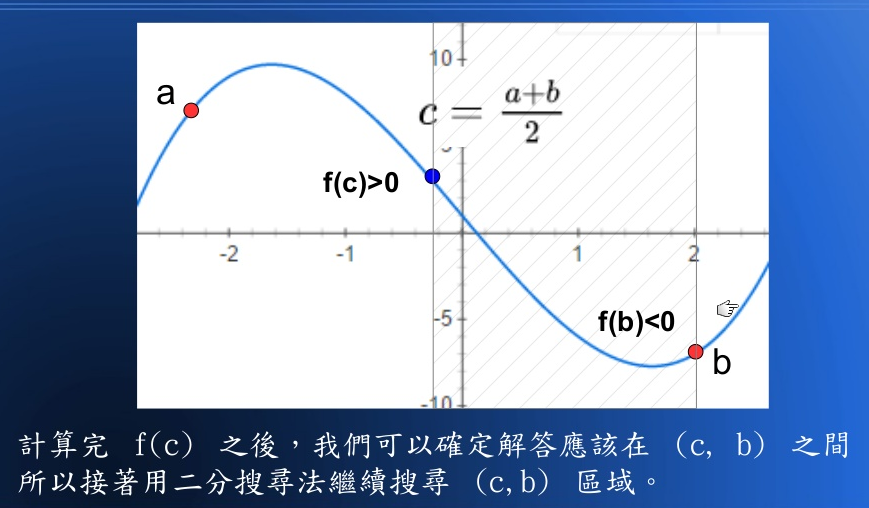
二分搜尋法求根的程式如下:
檔案: binarySearch.js
function f(x) {
return x*x-4*x+1;
}
function bsolve(f,a,b) {
var c = (a+b)/2;
if (Math.abs(a-b) < 0.00001)
return c;
if (f(c)*f(a)>=0)
return bsolve(f, c, b);
else
return bsolve(f, a, c);
}
var x=bsolve(f, 0, 1);
console.log("x=", x, " f(x)=", f(x));
執行結果:
D:\Dropbox\gitbook\rlab\code\solveEquation>node binarySearch.js
x= 0.2679481506347656 f(x)= 0.0000036088895285502076
當然, 我們也可以改用另一種中間值的取法,像是用《線性內插法》在某些狀況下會更好!
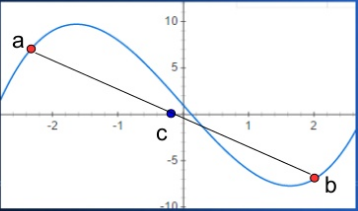
以上的這種搜尋法,不管是二分搜尋法,或者是線性內插法,速度通常都不會太慢!
如果您學過演算法中的 Big O 的複雜度概念,就會知道二分搜尋法的複雜度為 O(log n),只是在此問題中 n 應該改為兩個邊界值之間的差,也就是 (b-a),所以複雜度是 O(log b-a)。
但是、二分搜尋法求根的一個小問題,是必須要先找出一組 (a,b),滿足 f(a) 和 f(b) 兩者正負號相反。
而且二分搜尋法並不是找出所有的根,而是只找出一個根,這和暴力法找範圍內全部的根有所不同!
合併排序
檔案: mergesort.js
function sort(array) {
var length = array.length,
mid = Math.floor(length * 0.5),
left = array.slice(0, mid),
right = array.slice(mid, length)
if(length === 1) return array
return merge(sort(left), sort(right))
}
function merge(left, right) {
var result = [];
while(left.length || right.length) {
if(left.length && right.length) {
(left[0] < right[0]) ? result.push(left.shift()) : result.push(right.shift());
} else if (left.length) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
return result;
}
module.exports = sort
測試程式:
const msort = require('./mergesort')
console.log(msort([3,7,2,9,5,1,8,4]))
執行結果
$ node sortTest
[ 1, 2, 3, 4, 5, 7, 8, 9 ]
結語
以上我們用『二分搜尋』與『合併排序』,示範了 『分割擊破法』 (Divide & Conquer) 的想法,當然還有更多問題可以使用『分割擊破法』來處理,像是『離散傅立葉轉換』DFT 若改用『分割擊破法』實作成『快速傅立葉轉換』FFT,那就可以將複雜度由原本的 O(n^2) 改進為 O(n log n) ,所以有時候我們還可以透過『分割擊破法』來加快演算法的速度!