迭代法 Iterative
迭代法
話說《迭代法》,感覺非常神奇,但是說穿了很簡單!
迭代法的關鍵,可以說是一種《函數不動點》的尋找,也就是尋找符合條件 x=f(x) 的 x 值。
透過反覆計算 x[k+1] = f(x[k]) 的方式,假如最後達到收斂,那麼我們就知道該 x 值會是 x=f(x) 的解答。
以下是迭代法的計算過程:
x2 =f(x1)
x3 =f(x2)
...
x[k+1] =f(x[k])
所謂的不動點,就是 x=f(x) 這樣一個方程式。我們從 k=0 開始反覆用 x[k+1] =f(x[k]) 去找下一個 x[k+1],當我們找到符合 x[k+1] =f(x[k]) 的 x 時, x 基本上就定住了,這時我們找到的 x 就是 x=f(x) 的一個解答!
問題是,如果我們並非想找 f(x)=x 的解,而是 f(x)=0 的解呢? 那該怎麼辦?
其實答案很簡單, 只要修改方程式,想辦法讓 x 出 現在其中一邊就行了。
舉例而言, 假如我們想要找 f(x)=0 的解, 那麼我們可以對兩邊各加一個 x ,變成 f(x)+x = x 該等式仍然會成立。這樣就可以進行迭代了!
當然、迭代的形式不只一種, 對於 f(x)=0,以下都是可以用的迭代形式。
\begin{aligned}
& x=f(x)+x \\
x^2=f(x)+x^2 \qquad & x=(f(x)+x^2)/x \\
3x^3=f(x)+3x^3 \qquad & x=(f(x)+3x^3)/(3x^2) \\
f(x)/4=0 \qquad & x= x-f(x)/4
\end{aligned}
於是、您只要選擇一個起點, 像是 x=3 ,然後開始反複套用迭代公式,看看是否會收斂就行了!
假如我們的迭代公式是 x=g(x),那麼只要隨便選一個起點,例如 x1=3,然後用 x2 =g(x1),x3=g(x2) … 一直算下去,直到收斂為止。
以下是一個迭代法的程式範例, 用來尋找 x*x-4*x+1 的解!
function f(x) { return x*x-4*x+1; }
function g(x) { return x-f(x)/4; }
function isolve(g, x) {
console.log("x=", x);
for (var i=0; i<100000; i++) {
if (Math.abs(x-g(x)) < 0.001)
return x;
x = g(x);
console.log("x=", x);
}
return x;
}
var x = isolve(g, 1)
console.log("x=", x, "f(x)=", f(x))
執行結果:
$ node iteration.js
x= 1
x= 1.5
x= 2.1875
x= 2.9287109375
x= 3.4630849361419678
x= 3.6779305535505813
x= 3.7240678179159414
x= 3.7309653577225825
x= 3.7309653577225825 f(x)= -0.0037589303643326133
這種迭代法,其實幾乎可以用來解所有的方程式,最大的問題是《可能不會收斂》!,
而且不同的迭代方法,收斂速度也常 常有差異
在此我們舉一個簡單的例子, 假如您想求某個數 n 的平方根。那麼可以用下列三種的迭代算式
- $
x = 3/x$ - $
x_{k+1} = x_k - \frac{1}{4} (x^2_k -3)$ - $
x_{k+1} = \frac{1}{2} (x_k + \frac{3}{x_k})$
然後實作這三種方法,程式碼如下:
檔案: iterative3.js
var f1 = (x) => 3 / x
var f2 = (x) => x - 1 / 4 * (x * x - 3)
var f3 = (x) => 1 / 2 * (x + 3 / x)
var x1, x2, x3
x1 = x2 = x3 = 1
for (var i = 0; i < 20; i++) {
x1 = f1(x1); x2 = f2(x2); x3 = f3(x3)
console.log('x1:', x1, 'x2', x2, 'x3', x3)
}
執行結果
$ node iterative3
x1: 3 x2 1.5 x3 2
x1: 1 x2 1.6875 x3 1.75
x1: 3 x2 1.7255859375 x3 1.7321428571428572
x1: 1 x2 1.7311742305755615 x3 1.7320508100147274
x1: 3 x2 1.7319331764233397 x3 1.7320508075688772
x1: 1 x2 1.73203504452438 x3 1.7320508075688772
x1: 3 x2 1.7320486956592371 x3 1.7320508075688772
x1: 1 x2 1.732050524625521 x3 1.7320508075688772
x1: 3 x2 1.7320507696616354 x3 1.7320508075688772
x1: 1 x2 1.7320508024902694 x3 1.7320508075688772
x1: 3 x2 1.732050806888473 x3 1.7320508075688772
x1: 1 x2 1.7320508074777203 x3 1.7320508075688772
x1: 3 x2 1.7320508075566647 x3 1.7320508075688772
x1: 1 x2 1.7320508075672412 x3 1.7320508075688772
x1: 3 x2 1.7320508075686583 x3 1.7320508075688772
x1: 1 x2 1.7320508075688479 x3 1.7320508075688772
x1: 3 x2 1.7320508075688732 x3 1.7320508075688772
x1: 1 x2 1.7320508075688767 x3 1.7320508075688772
x1: 3 x2 1.7320508075688772 x3 1.7320508075688772
x1: 1 x2 1.7320508075688772 x3 1.7320508075688772
這三種方法的收斂情形如下圖:
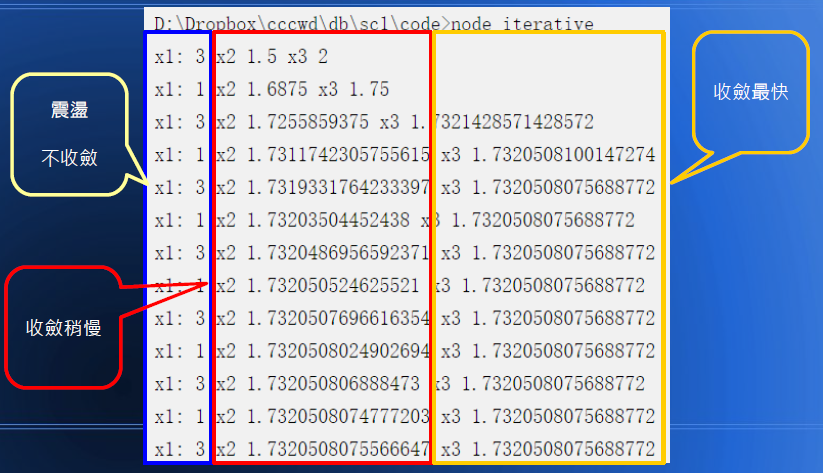
因此、好的迭代算式可以讓你上天堂,不好的迭代算式會讓你住牢房!
如果想要確定迭代法會收斂, 必須要好好的設計《迭代函數》 與《初始值》才行!
當然、有人可能會問, 假如我想解的不是方程式,而是像下列的這種《方程組》的話,那該怎麼辦呢?
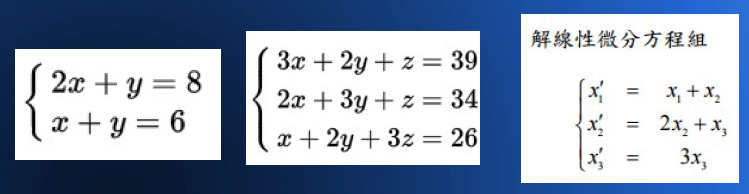
其實這個問題, 只要稍微轉換一下,就可以讓 《方程組變成單一的方程式》
假如您想求解下列方程組
f(x)=0
g(x)=0
那麼只要改寫為
$f^2(x) +g^2(x) = 0$
就可以《將方程組變成方程式》了。
只是這樣一來,線性的方程組就有可能變成了 《二次的非線性方程式》
這就是,用解方程式的方法來解方程組,所需要付出的代價了。
不過迭代法確實是一個,很好的《數值方法》 可以用來解很多方程式。
結語
您可以看到迭代法可以用來求方程式的解,也可以用來尋找馬可夫鏈的平衡機率,當然還有很多領域的問題,都可以用迭代法來解決。
例如 EM 演算法,就是用迭代法來求最大機率模型的方法。
另外還有 KMEAN 演算法,則是用迭代進行機器學習的方法。