蒙地卡羅法 Monte-Carlo
蒙地卡羅演算法 (Monte Carlo Algorithm)
利用亂數隨機抽樣的方式以計算某種解答的演算法,被稱為蒙地卡羅演算法,其中最簡單的方法是直接取樣算法。
用蒙地卡羅法算 Pi
舉例而言,假如我們不知道半徑為 1 的圓形面積,那麼就可以利用亂數隨機取樣 1百萬個介於 0 到 1 之間的 (x,y) 值,然後看看有多少點落在圓內 (x^2 + y^2 <=1) 來計算 P。最後利用 4 * P(在圓之內) 就可以計算出該圓形的面積。

上圖來自維基百科 https://upload.wikimedia.org/wikipedia/commons/thumb/8/84/Pi_30K.gif/330px-Pi_30K.gif
以下是用用蒙地卡羅法計算 Pi 的程式碼。
function monteCarloPi(n) {
let hits = 0
for (let i=0;i<n; i++) {
let x = Math.random()
let y = Math.random()
if (x*x+y*y <= 1) hits++
}
return 4*(hits/n)
}
console.log('MonteCarloPi(100000)=', monteCarloPi(100000))
執行結果
$ node monteCarloPi.js
MonteCarloPi(100000)= 3.14056
$ node monteCarloPi.js
MonteCarloPi(100000)= 3.14228
$ node monteCarloPi.js
MonteCarloPi(100000)= 3.14628
馬可夫鏈
「馬可夫鏈」是一種具有狀態的隨機過程,有點像是「有限狀態機」,但是「從目前狀態轉移 s 到下一個狀態 s’ 的機率」由 Q(s=>s’) 所表示,這個狀態之轉移機率並不會受到狀態以外的因素所影響,因此與時間無關。
隨機漫步就是馬可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點,每一步可以移動到任何一個相鄰的點,在這裡移動到每一個點的概率都是相同的(無論之前漫步路徑是如何的)。
假如我們不斷的觀察某種隨機現象,會看到許多一連串的觀察值 x1, x2,…, xn ,這些觀察值會形成整個隨機現象空間 X1, X2,…, Xn。
假如這些觀察值之間有某種因果關係,那麼我們就有可能透過馬可夫過程描述此因果關係,舉例而言,如果每個事件只受到前一個事件的影響,那麼就可以用 P(X[n+1] | X[n]) 表示此隨機現象,這種隨機過程稱為時間無關的馬可夫鏈 (Time-homogeneous Markov chains, 或稱為穩定型馬可夫鏈 stationary Markov chains)。
假如下一個觀察值可能受前 m 個觀察值所影響,那麼此種隨機過程可由機率分布 P(X[n+1] | X[n], …, X[n-m+1’) 表示,因此稱為 m 階的馬可夫過程。
以下我們只討論一階馬可夫鏈,也就是每個事件只受到前一個事件的影響的情況,這可以用 P(X[n+1] | X[n]) = Q(s=>s’) 描述。
計算馬可夫鏈機率
對於一個具有「馬可夫特性」的「機率式有限狀態機」,我們可以用「機率轉移矩陣」進行描述,舉例而言:下圖顯示了一個只有兩個狀態的「馬可夫隨機系統」。
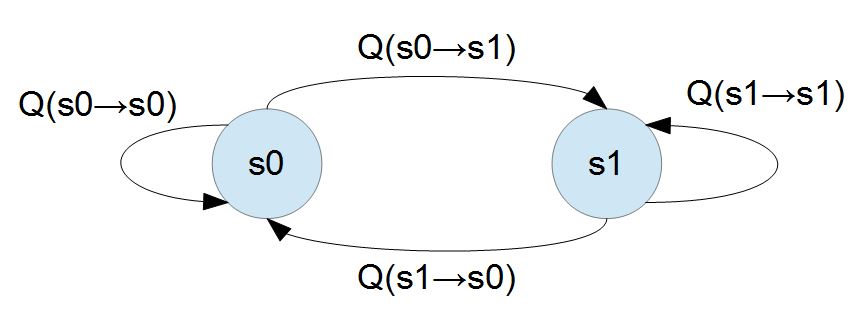
若要用機率模型描述上述兩個狀態的馬可夫系統,我們需要給定兩組機率值,第一組是狀態本身的機率 P(s0)、P(s1)。第二組是狀態轉移的機率 Q(s0=>s0)、Q(s0=>s1)、Q(s1=>s0)、Q(s1=>s1) 。
以下是上圖的機率分佈描述程式 prob.js : (我們把 P, Q 全部整合在單一的 P 陣列中)
// 狀態機率: P(a) = 0.2, P(b) = 0.8
// 轉移機率: P(x => y)
// a b
// a 0.7 0.3
// b 0.5 0.5
const P = {
'a': 0.2, 'b': 0.8,
'a=>a': 0.7, 'a=>b':0.3,
'b=>a': 0.5, 'b=>b':0.5,
}
module.exports = P
有了這上述機率分佈 P, 我們就可以輕鬆地計算任意序列的出現機率了。
假如
// 參考: 自然語言處理 -- Hidden Markov Model http://cpmarkchang.logdown.com/posts/192352
const P = require('./prob')
function markov(s) {
let p = P[s[0]]
for (let i=1; i<s.length; i++) {
let key = s[i-1]+'=>'+s[i]
p = p * P[key]
}
return p
}
const seq = ['b', 'a', 'b', 'b']
console.log('P(%j)=%d', seq, markov(seq))
執行結果:
$ node markov.js
P(["b","a","b","b"])=0.06
上述馬可夫鏈的機率,是用確定性的計算方法算出的,並不算是『蒙地卡羅法』,因為所謂的蒙地卡羅法是用『亂數』模擬後進行統計的方法,上述方法沒有『亂數模擬』。
蒙地卡羅馬可夫算法 (Monte Carlo Markov Chain, MCMC)
接著我們用『亂數模擬』的方法來模擬上述『馬可夫鏈』問題,程式碼如下:
const P = require('./prob')
const rnd = Math.random
function mcmc(s) { // Monte Carlo Markov Chain
if (rnd() > P[s[0]]) return 0
for (let i=1; i<s.length; i++) {
let key = s[i-1]+'=>'+s[i]
if (rnd() > P[key]) return 0
}
return 1
}
function markov(s, n) {
let pass = 0
for (let i=0; i<n; i++) {
pass += mcmc(s)
}
return pass/n;
}
const seq = ['b', 'a', 'b', 'b']
console.log('P(%j)=%d', seq, markov(seq, 100000))
執行結果
$ node mcmc
P(["b","a","b","b"])=0.06019
$ node mcmc
P(["b","a","b","b"])=0.06103
$ node mcmc
P(["b","a","b","b"])=0.05955
結語
當問題很單純,而且我們知道簡單明確的算式時,不需要使用『蒙地卡羅法』,但是若問題很複雜,沒有明確簡單的算式時,用蒙地卡羅法就是個好的選擇!
透過隨機模擬的方式,可以用統計法計算出很多分布的機率,這就是蒙地卡羅法!
習題
- 請設計出一個蒙地卡羅 gibbs 算法,算出『馬可夫粗略平衡』(「一般平衡狀態」) 時各個狀態的機率!
- 『馬可夫粗略平衡』請參考下列描述!
習題 1 的背景知識 – 馬可夫平衡
長期來看、馬可夫系統通常最後會達到一個穩定平衡,在平衡的情況之下,每個節點的輸出將會等於該節點的輸入,這就是所謂的「一般平衡條件」。
讓我們用下圖的範例來說明「馬可夫系統」達到穩定平衡時的狀況。
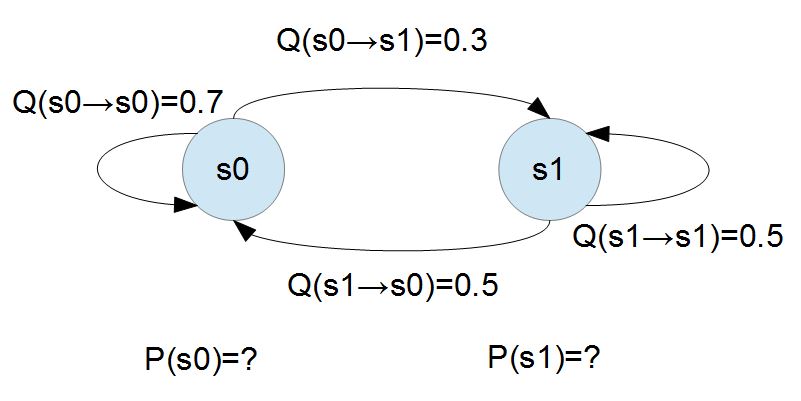
對於上述有「馬可夫隨機系統」,我們可以用「二元一次聯立方程式」求解 P(s0) 與 P(s1),假如我們將 P(s0) 寫為 P0,P(s1) 寫為 P1,那麼整個系統達到平衡時,應該會有下列狀況。
P0*0.3 = P1*0.5 ; P0 的流出量 = P0 的流入量
P0+P1 = 1 ; 狀態不是 s0 就是 s1
如果我們求解上述方程式,就可以得到 (P0=5/8, P1=3/8),此時整個系統會達到平衡。
假如我們模擬機率性粒子在馬可夫鏈中的移動行為,最後這些移動將達到一個平衡。在達到平衡後,從 x 狀態流出去的粒子數,將會等於流回該狀態的粒子數,也就是必須滿足下列『平衡條件』的要求。
$$\sum_y P(x) Q(x \to y) = \sum_y P(y) Q(y \to x)$$
當隨機的粒子移動時,如果從 x 流出的粒子較多,自然會讓 P(x) 下降,最後仍然達到平衡,如果流入 x 的粒子比流出的多,那麼 P(x) 自然就會上升,只要我們能模擬流出流入的程序,最後整個馬可夫系統將會達到平衡。
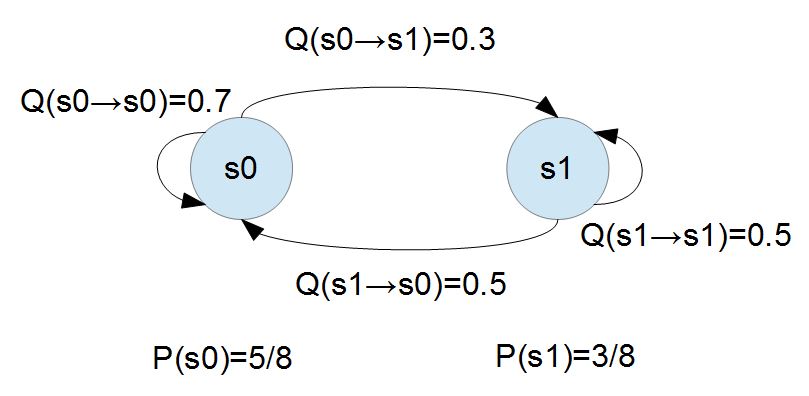
上圖顯示了上述馬可夫系統處於「一般平衡狀態」時的狀況,您可以發現其中的「節點 s0 的總流出」為 $$(5/80.3 = 15/80)$$ ,而「節點 s0 的總流入」$$(3/80.5 = 15/80)$$,其計算過程如下所示。
$\sum_y P(x) Q(x \to y) = 5/8 * 0.3 = 15/80 = 3/8*0.5 = \sum_y P(y) Q(y \to x)$
運用上述的「一般平衡條件」,當我們已經知道「轉移矩陣」$$Q(x \to y)$$ 的每個數值,但是卻不知道達成平衡的節點機率 P(x) 時,可以設計出一種稱為 「Gibbs 演算法」的學習程式,該算法可以尋找出每個節點達到平衡時的機率值。
用迭代法求解馬可夫鏈的平衡機率 – Gibbs Algorithm
// Gibbs Algorithm 的範例
// 問題:機率式有限狀態機,P(a=>b)=0.3, P(b=>a)=0.5 ; P(a=>b)=0.7, P(b=>b)=0.5
// 目標:尋找該「機率式有限狀態機」的穩態,也就是 P(a) = ?, P(b)=? 時系統會達到平衡。
const P = require('./prob')
function gibbs (P) {
var P0 = {'a': P['a'], 'b': P['b'] }
do {
var P1 = { // 下一輪的機率分布。
'a': P0['a'] * P['a=>a'] + P0['b'] * P['b=>a'],
'b': P0['a'] * P['a=>b'] + P0['b'] * P['b=>b']
}
console.log('P1 = %j', P1)
var da = P1['a'] - P0['a'], db = P1['b'] - P0['b'] // 兩輪間的差異。
var step = Math.sqrt(da * da + db * db) // 差異的大小
P0 = P1
} while (step > 0.001) // 假如差異夠小的時候,就可以停止了。
console.log('標準答案:P(a)=5/8=%d P(b)=3/8=%d', 5 / 8, 3 / 8) // 印出標準答案,以便看看我們找到的答案是否夠接近。
}
gibbs(P)
執行結果
$ node gibbs
P1 = {"a":0.54,"b":0.46}
P1 = {"a":0.608,"b":0.392}
P1 = {"a":0.6215999999999999,"b":0.37839999999999996}
P1 = {"a":0.62432,"b":0.37567999999999996}
P1 = {"a":0.624864,"b":0.37513599999999997}
標準答案:P(a)=5/8=0.625 P(b)=3/8=0.375
習題 1 解答
const P = require('./prob')
const rnd = Math.random
function mcmc() { // Monte Carlo Markov Chain
let s1 = (rnd() < P['a']) ? 'a' : 'b'
let s2 = (rnd() < P[s1+'=>'+'a']) ? 'a' : 'b'
if (s1 == s2) return
P[s1] -= 0.0001
P[s2] += 0.0001
}
function gibbs(n) {
for (let i=0; i<n; i++) {
mcmc()
}
}
console.log("P=%j", P)
gibbs(1000000)
console.log('P=%j', P)
執行結果
$ node mcmcGibbs
P={"a":0.2,"b":0.8,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
P={"a":0.6301999999999527,"b":0.3698000000000474,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
$ node mcmcGibbs
P={"a":0.2,"b":0.8,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
P={"a":0.6163999999999542,"b":0.3836000000000459,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
$ node mcmcGibbs
P={"a":0.2,"b":0.8,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
P={"a":0.6220999999999536,"b":0.37790000000004653,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
$ node mcmcGibbs
P={"a":0.2,"b":0.8,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}
P={"a":0.618499999999954,"b":0.38150000000004614,"a=>a":0.7,"a=>b":0.3,"b=>a":0.5,"b=>b":0.5}