陳鍾誠

Version 1.0

Gibbs 演算法

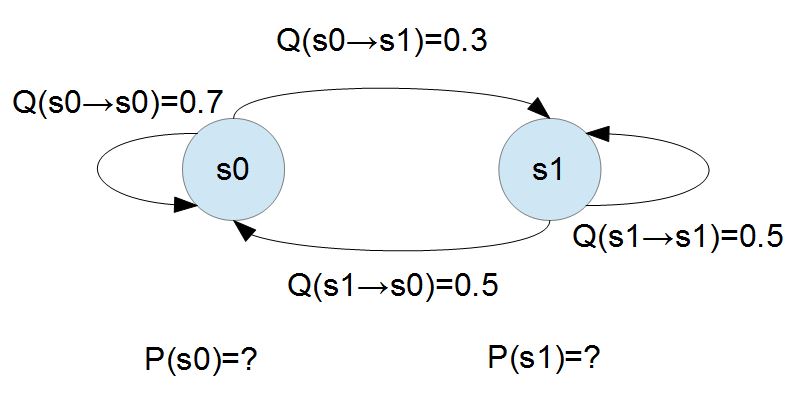
如前所述、我們可以用 Gibbs 演算法，在已知「轉移矩陣」的情況下求解「每個狀態的平衡機率值」，我們將用下圖這個只有兩個狀態的馬可夫系統為例，將「Gibbs 演算法」轉換為實際的 JavaScript 程式，讓讀者透過程式實際體會 Gibbs 演算法的原理。

圖、只有兩個狀態的馬可夫隨機系統，何時會達到平衡呢？

程式範例

現在、我們希望用 Gibbs 演算法來尋找上述問題的穩態，一開始我們可以隨意設定一個初始的隨機分布，例如 (P0, P1) = (0.5, 0.5)。

接著我們就可以用疊代的方法，計算該系統的穩態，以下的 JavaScript 程式就模擬了這種過程。

檔案： gibbs.py

# Gibbs Algorithm 的範例
# 問題：機率式有限狀態機，P(a=>b)=0.3, P(b=>a)=0.5 ; P(a=>b)=0.7, P(b=>b)=0.5
# 目標：尋找該「機率式有限狀態機」的穩態，也就是 P(a) = ?, P(b)=? 時系統會達到平衡。
from prob import P
import math

def gibbs (P):
    P0 = {'a': P['a'], 'b': P['b'] }
    print('P0 = {}'.format(P0))
    while True:
        P1 = { # 下一輪的機率分布。
            'a': P0['a'] * P['a=>a'] + P0['b'] * P['b=>a'], 
            'b': P0['a'] * P['a=>b'] + P0['b'] * P['b=>b']
        }
        print('P1 = {}'.format(P1))
        da = P1['a'] - P0['a']
        db = P1['b'] - P0['b'] # 兩輪間的差異。
        step = math.sqrt(da * da + db * db) # 差異的大小
        P0 = P1
        if (step < 0.001): break # 假如差異夠小的時候，就可以停止了。

    print('標準答案:P(a)=5/8={} P(b)=3/8={}'.format(5 / 8, 3 / 8)) # 印出標準答案，以便看看我們找到的答案是否夠接近。

gibbs(P)

執行結果：

$ python3 gibbs.py
P0 = {'a': 0.2, 'b': 0.8}
P1 = {'a': 0.54, 'b': 0.46}
P1 = {'a': 0.608, 'b': 0.392}
P1 = {'a': 0.6215999999999999, 'b': 0.37839999999999996}
P1 = {'a': 0.62432, 'b': 0.37567999999999996}
P1 = {'a': 0.624864, 'b': 0.37513599999999997}
標準答案:P(a)=5/8=0.625 P(b)=3/8=0.375

您可以看到上述程式所找到的答案 [0.6248,0.3752] 與我們用「聯立方程式」求出來的答案 [5/8, 3/8] 之間非常接近，這代表上述的 Gibbs 程式可以求出系統的穩態。

當然、上述的算法只是一個極度簡化的範例，還不能完全代表 Gibbs Algorithm，現在讓我們用比較抽象但通用的講法來說明 Gibbs 演算法。

數學描述

Gibbs 取樣程序的使用時機是在聯合分布 P(X,Y) 未知，但是單一變數的條件機率 $Q(X \to Y), Q(Y|X), P(X), P(Y) 已知的情況。在此種情況下，我們可以利用亂數產生的樣本，統計聯合機率分布。

該程序首先取得一個分布 Y0 作為初始值，然後利用蒙地卡羅法透過 (X, Y0) 產生 X1 分布，接著再利用 (X1, Y) 產生 Y1 分布。於是我們得到下列這個疊代程序

Algorithm GibbsSampling(X, Y)
　Y[0] = random initialize a distribution
　for i = 1 to N
　　generate X[i] from Y[i-1] and Q(Y[i-1]→X)
　　generate Y[i] from X[i] and Q(X[i]→Y) 
　return {X[N], Y[N]}
End Algorithm

以上疊代程序是針對兩個隨機變數的情況，假如我們希望延伸到 k 個隨機變數的情況，可以修改演算法如下。

Algorithm GibbsSampling(X[1...k])
　X = random initialize a distribution
　for i = 1 to N
　　generate X'[1] from X and Q(X[2], ..., X[k] → X[1])
    ...
　　generate X'[j] from X and Q(X[1], ..., X[j-1], X[j+1],...,X[k] → X[i])
    ...
　　generate X'[k] from X and Q(X[1], ..., X[k-1] → X[k])
    X = X'
  end
　return X
End Algorithm

Gibbs 取樣程序是『蒙地卡羅馬可夫算法』(MCMC) 的一個案例，也是 Metropolis-Hasting 取樣程序的一個特例，我們可以利用 Gibbs 或 Metropolis-Hasting 取樣程序計算貝氏網路的聯合機率分布。

參考文獻


 Edit on GitHub