實作:深度與廣度搜尋法
簡介
為了進一步理解深度優先搜尋 (Depth-First Search) 與廣度優先搜尋 (Breath-First Search) ,我們將在本文中採用 python 實作這兩個圖形搜尋算法。
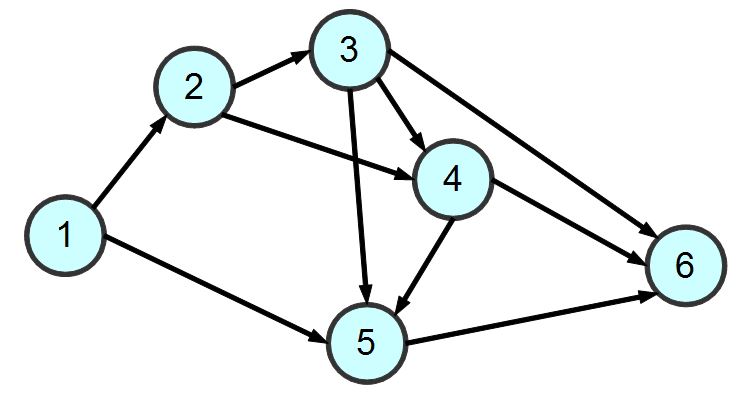
在以下程式中,變數 g 代表下列圖形,而程式中的 dfs() 函數代表深度優先搜尋算法,bfs() 函數代表廣度優先搜尋算法。
程式實作
檔案:graph_search.py
def enqueue(a, o):
a.insert(0, o)
def dequeue(a):
return a.pop()
g = { # graph: 被搜尋的網路
'1': {'n':['2','5'], 'v':0}, # n: neighbor (鄰居), v: visited (是否被訪問過)
'2': {'n':['3','4'], 'v':0},
'3': {'n':['4','5','6'], 'v':0},
'4': {'n':['5','6'], 'v':0},
'5': {'n':['6'], 'v':0},
'6': {'n':[], 'v':0}
}
def init(g): # 初始化、設定 visited 為 0
for i in g:
g[i]['v'] = 0
def dfs(g, node): # 深度優先搜尋
if g[node]['v']!=0: # 如果已訪問過,就不再訪問
return
print(node, '=> ', end = '') # 否則、印出節點
g[node]['v'] = 1 # 並設定為已訪問
neighbors = g[node]['n'] # 取出鄰居節點
for n in neighbors: # 對於每個鄰居
dfs(g, n) # 逐一進行訪問
queue=['1'] # BFS 用的 queue, 起始點為 1。
def bfs(g, q): # 廣度優先搜尋
if len(q)==0: # 如果 queue 已空,則返回。
return
node = dequeue(q) # 否則、取出 queue 的第一個節點。
if g[node]['v'] == 0: # 如果該節點尚未拜訪過。
g[node]['v'] = 1 # 標示為已拜訪
else: # 否則 (已訪問過)
return # 不繼續搜尋,直接返回。
print(node, '=> ', end = '') # 印出節點
neighbors = g[node]['n'] # 取出鄰居。
for n in neighbors: # 對於每個鄰居
if not g[n]['v']: # 假如該鄰居還沒被拜訪過
enqueue(q, n) # 就放入 queue 中
bfs(g, q)
print('dfs:', end = '')
init(g)
dfs(g, '1') # 呼叫深度優先搜尋。
print('')
print('bfs:', end = '')
init(g)
bfs(g, queue) # 呼叫廣度優先搜尋。
print('')
執行結果
mac020:04-graphSearch mac020$ python3 graph_search.py
dfs:1 => 2 => 3 => 4 => 5 => 6 =>
bfs:1 => 2 => 5 => 3 => 4 => 6 =>
結語
從以上範例您可以看到 BFS 與 DFS 之差異,不過我們沒有為節點加入好壞的評估函數,因此沒有實作最佳優先搜尋,或許讀者可以自行嘗試修改看看。
【本文由陳鍾誠取材並修改自 [維基百科],採用創作共用的 [姓名標示、相同方式分享] 授權】