平均值的估計與檢定
在上一章當中,我們說明了中央極限定理的意義,也就是對於某母體 (平均數 mean、標準差 sd) 而言,抽出 n 個獨立樣本 $x_1, …, x_n$ , 其平均數 $\bar{x}=\frac{x_1+…+x_n}{n}$ 會趨近於常態分布 N(mean, sd/n) 。
換句話說,也就是 $\frac{\bar{x}-mean}{sd/\sqrt{n}}$ 會趨近於標準常態分布 $Z=N(0, 1)$ 。
有了這樣的定理當基礎,我們就可以進行估計了!但在這之前,我們必須先理解一個關念,那就是信賴區間。
信賴區間
對於一個機率分布 X 而言,假如其機率密度函數為 P(x),那麼該機率分布在 L1 ≤ x ≤ L2 這個區域之間的機率總和,可以寫成如下算式:
| 分布類型 | P(L1 ≤ x ≤ L2) |
|---|---|
| 離散情況 | $\sum_{x=L1}^{L2} P(x)$ |
| 連續情況 | $\int_{L1}^{L2} P(x) dx$ |
由於是機率分布,所以上述算式的總和必然介於 0 到 1 之間,假如我們稱該總和為 $\beta$ ,那麼該區間就是一個機率值為 $\beta$ 的信賴區間。
補充:我們經常將該 $\beta$ 寫為 $\beta=1-\alpha$ ,然後稱該區間為 $100(1-\alpha)%$ 的信賴區間。
為了瞭解信賴區間的慨念,先讓我們看看常態分配 (Normal) 與均等分配 (Uniform) 等兩個機率分布的圖形:
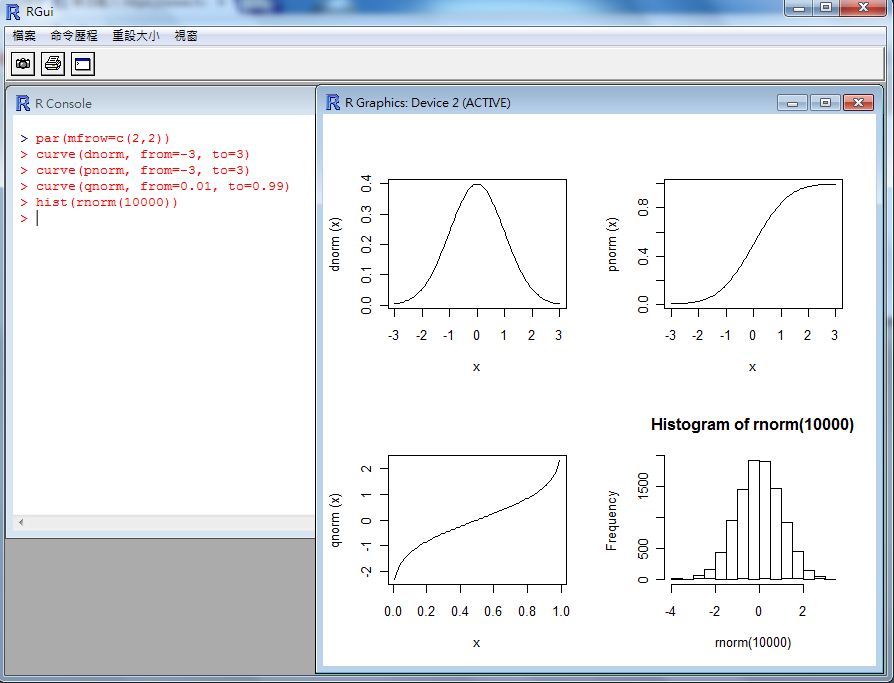

接著讓我們先用均等分配為例,說明信賴區間的概念。舉例而言,假如對於一個介於 0 到 10 之間的均等分布而言, 由於每個點的機率密度函數為 1/10,因此介於 (1, 9) 之間的機率將會是 0.8,也就是 80%。 因此 (1, 9) 是該機率母體的 80% 信賴區間,以下是我們用 R 軟體反應這個信賴區間的操作過程。
> L2=punif(9, min=0, max=10)
> L2
[1] 0.9
> L1=punif(1, min=0, max=10)
> L1
[1] 0.1
> L2-L1
[1] 0.8
常態分布的信賴區間
根據中央極限定理,在樣本數夠多 (通常 > 20) 的情況之下,平均值 $\bar{X}$ 會趨近於常態分布, 因此常態分布的信賴區間對估計 $\bar{X}$ 相當重要,所以我們接下來要看看常態分布的信賴區間。
假如您已經知道某母體為常態分布,而且期望值 (平均值) 為 mean ,標準差為 sd , 那麼當您用該母體來產生樣本,有多少的樣本會落在範圍 (L1, L2) 之外呢?
上述問題感覺數學符號多了一點,讓我們用實際的數字來進一步說明。
假如母體為標準常態分布 Z=N(0, 1) ,那麼請問產生的樣本落在 (-2, 2) 之外的會有多少呢?
這個問題讓我們用 R 軟體來實際操做看看。
> L2=pnorm(2, mean=0, sd=1)
> L1=pnorm(-2, mean=0, sd=1)
> L1
[1] 0.02275013
> L2
[1] 0.9772499
> L2-L1
[1] 0.9544997
> 1.0-(L2-L1)
[1] 0.04550026
以上的操作告訴我們,標準常態分布 Z 的樣本落在 (-2, 2) 之內的機率約為 0.9544997,因此落在範圍外的機率為 0.04550026。
那麼,假如不是標準常態分布,那又如何呢?其實只要知道平均值 mean 與標準差為 sd ,就可以輕易的用 R 軟體算出來。 舉例而言,假如某母體為常態分布 N(mean=5, sd=3) ,那麼若我們想知道其樣本落在 (3, 6) 之間的機率有多少,就可以用 下列操作計算出來。
> L2=pnorm(6, mean=5, sd=3)
> L1=pnorm(3, mean=5, sd=3)
> L1
[1] 0.2524925
> L2
[1] 0.6305587
> L2-L1
[1] 0.3780661
根據上述操作,我們知道樣本落在 (3, 6) 之間的機率為 0.3780661。
當然、如果我們真的去用 N(mean=5, sd=3) 的隨機函數產生樣本,其統計值並不一定會那麼的準,但是樣本越多的話, 統計值就會越準,請看下列操作。
操作:產生 10 個樣本的情況
> x=rnorm(10, mean=5, sd=3)
> x
[1] 6.387168 7.292018 4.680202 2.225559 11.208245 7.040107 2.739477
[8] 2.316105 4.482658 4.913032
> 3<x
[1] TRUE TRUE TRUE FALSE TRUE TRUE FALSE FALSE TRUE TRUE
> x<6
[1] FALSE FALSE TRUE TRUE FALSE FALSE TRUE TRUE TRUE TRUE
> 3<x & x<6
[1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE TRUE TRUE
> sum(3<x & x<6)
[1] 3
> sum(3<x & x<6)/10
[1] 0.3
操作:產生 100 個樣本的情況
> x=rnorm(100, mean=5, sd=3)
> sum(3<x & x<6)
[1] 34
> sum(3<x & x<6)/100
[1] 0.34
操作:產生 100000 個樣本的情況
> x=rnorm(100000, mean=5, sd=3)
> sum(3<x & x<6)
[1] 37865
> sum(3<x & x<6)/100000
[1] 0.37865
以上的操作大致反映出了「大數法則」,樣本越多就會越接近母體的分布。
但是,如果我們先給定要求的機率,而不是先給定區間,那麼要如何找出符合該機率的區間呢?
舉例而言,假如我們想知道常態分布 N(mean=5, sd=3) 的 98% 信賴區間,那麼應該怎麼作呢?以下是我們的操作。
> L1=qnorm(0.01, mean=5, sd=3)
> L1
[1] -1.979044
> L2=qnorm(0.99, mean=5, sd=3)
> L2
[1] 11.97904
> P1=pnorm(L1, mean=5, sd=3)
> P1
[1] 0.01
> P2=pnorm(L2, mean=5, sd=3)
> P2
[1] 0.99
> P2
在上述操作中,我們先將 (100-98)% = 2% ,平均分配到常態分配的兩端,然後透過 qnorm(0.01, mean=5, sd=3)
找出下界 L1,接著透過 L2=qnorm(0.99, mean=5, sd=3) 找出上界 L2,如此就找出了該常態分布的 98% 信賴區間,為
(L1=-1.979044, L2=11.97904)。
為了驗證這個答案是正確的,我們再度用 P1=pnorm(L1, mean=5, sd=3) 找出 L1 之前的累積機率,發現確實是 0.01 (也就是 1%),
而 L2 之前的累積機率是 0.99 (99%),因此該區間的機率就是 P2 - P1 = 0.99-0.01 = 0.98。
接著,我們可以利用該母體產生很多樣本,以驗證看看這些樣本落於信賴區間內的機率是否符合 98% 的條件,以下是對應的 R 軟體操作。
> x = rnorm(100000, mean=5, sd=3)
> p = sum(L1<x & x<L2)/100000
> p
[1] 0.98012
在上述操作中,您可以看到當我們產生十萬個樣本時,這些樣本落在信賴區間內的機率為 0.9812,相當接近 0.98 這個預期值,這用實驗 驗證了上述信賴區間的機率應該是對的。
平均值的信賴區間
按照上述的方法,若我們知道母體為何,那麼就很容易找出一個信賴區間符合特定的機率要求,但是在統計的情況之下,我們往往不知道 母體為何?
如果我們知道母體是 N(mean=5, sd=3),那麼我們根本不需要計算平均數,因為 mean=5 就告訴了你母體的平均數是 5。
但是當我們不知道母體平均數的時候,如何用樣本 $x_1, x_2, …, x_n$ 去推測 (或說猜測) 母體的平均數 mean 呢?
這個情況有點像下述的 R 程式,讓我們看看以下操作:
> x = rnorm(25, mean=mu, sd=2)
> x
[1] 10.829923 7.786320 6.975080 6.980363 8.999509 7.343410 5.928051 9.158911
[9] 10.116548 7.042043 8.434972 10.530158 7.258413 8.990531 8.484475 9.104462
[17] 1.223568 7.011966 6.405762 4.449411 11.465473 7.382751 10.305355 10.201814
[25] 11.802796
> mean(x)
[1] 8.168483
> sd(x)
[1] 2.332146
>
在上述操作中,我們知道標準差 sd=2,但是不知道平均數 mean=mu (由於程式中沒辦法打數學符號, 以下的 mu 其實都代表數學符號 $\mu$) 中的 mu 是多少,不過我們可以觀察到 25 個樣本序列 $x_1, x_2, …, x_{25}$ 的值,而且可以計算出這些樣本的平均值 mean(x) = 8.168483 與 樣本變異數 sd(x) = 2.332145。
問題是,母體的平均值 mean (也就是 mu) 到底是多少呢?
這時我們必需要猜測 (或說推測)!
一個最簡單的推測是,我們認為 mean(x) 的值 8.168483 來取代母體的 mean ,也就是直接認為「樣本的平均值 = 母體的平均值」, 這種推測方法雖然很簡單,但是卻通常不錯。
這種以單一數值推測母體參數的方法,稱為「點估計」。
但是「點估計」太過武斷,事實上筆者用來產生上述樣本時,所設定的 mu 值為 8.0,而不是 8.168483 (不過您可以看到其實蠻接近的)。
如果我們將「估計的方法」改變一下,不要硬用一個點套上去,而是改去推測 mu 的可能範圍,那麼這種估計方法就會變化為「區間估計」。
當母體的標準差 $sd=\sigma$ 為已知的時候,根據中央極限定理,平均值會趨近於常態分布,因此我們可以用常態分布來進行「信賴區間估計」,這就是尚未正規化之前的中央極限定理,如下公式所示:
$\bar{x}=\frac{x_1+…+x_n}{n} \to N(\mu, \sigma/n)$
但是、如果我們將上述的平均值進行正規化,也就是移項並調整之後,改用下式表示:
$\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \to Z=N(0, 1)$
那麼我們就可以用下列程式來估計這種母體標準差已知情況下的平均值 $\mu$ 了。
mean.range = function(x, alpha=0.05, sd) {
n = length(x) # n = 樣本數
mx = mean(x) # mx 即為平均值 mu 的點估計
r1 = qnorm(alpha/2) # 信賴區間,下半截掉 alpha/2
r2 = qnorm(1-alpha/2) # 信賴區間,上半截掉 alpha/2
L1 = mx-r2*sd/sqrt(n) # 信賴區間下限
L2 = mx-r1*sd/sqrt(n) # 信賴區間上限
range = c(L1, mx, L2) # 信賴區間
}
於是我們可以用這個程式去進行區間估計,得到下列操作結果。
> mean.range = function(x, alpha=0.05, sd) {
+ n = length(x) # n = 樣本數
+ mx = mean(x) # mx 即為平均值 mu 的點估計
+ r1 = qnorm(alpha/2) # 信賴區間,下半截掉 alpha/2
+ r2 = qnorm(1-alpha/2) # 信賴區間,上半截掉 alpha/2
+ L1 = mx-r2*sd/sqrt(n) # 信賴區間下限
+ L2 = mx-r1*sd/sqrt(n) # 信賴區間上限
+ range = c(L1, mx, L2) # 信賴區間
+ }
> mean.range(x, sd=2)
> R = mean.range(x, sd=2)
> R
[1] 7.384497 8.168483 8.952468
上述操作代表根據樣本 x 所推估的 95% 的信賴區間 ( alpha=0.05, 1-alpha=0.95) 為 (7.384497, 8.952468), 而樣本的平均值 mean(x) 為 8.168483。
現在我們已經學會的信賴區間估計的方法,但是卻還有一個缺憾!
通常我們除了不知道母體的平均值 mu 之外,我們也不會知道母體的標準差 sd ,因此上述的推估程式其實沒有太大的實用價值!
(這也是為何 R 軟體預設的套建沒有納入這類函數的原因之一)。
T 分佈與平均值的檢定
當母體標準差 sd 未知的時候,我們就無法用常態分布來進行推估了,而必需要用一種稱為 T 分配的分布,來推估母體平均值 mean 的範圍。
那麼、T 分布到底是甚麼呢?其實 T 分布只是常態分布考慮「標準差」未知情況下的一種調整後的結果而已。
因為當標準差 $\sigma$ 未知時,我們只能改用「樣本標準差 S」 來估計「母體標準差 \sigma」,因此我們可以列出下列兩個算式。
$\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim N(0,1)$
$\frac{(n-1) S^2}{\sigma^2} \sim \chi (n-1)$
當上述兩個分佈互相獨立時,我們就可以得到一種經由卡方 ( $\chi^2$ ) 分布調整過的常態分布,稱為 T ,其定義如下:
$T=\frac{\bar{X} - \mu}{S/\sqrt{n}} \sim t(n-1)$
讓我們些看看 T 分布到底長得什麼樣?
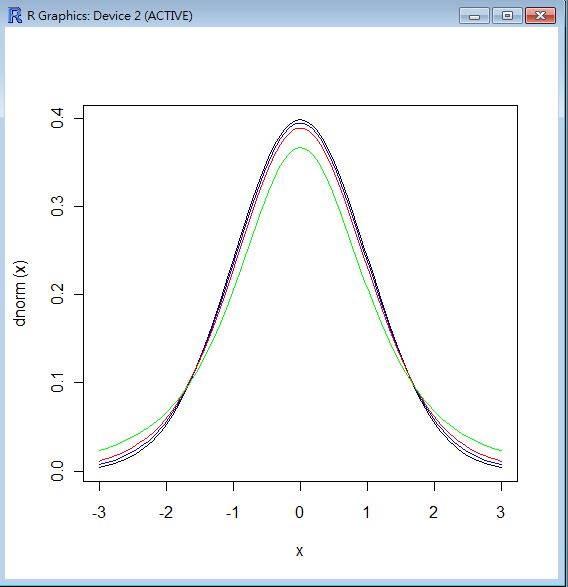
其實 T 分布與常態分布非常接近,只是考慮到樣本數量 (自由度+1) 的影響力,因此稍微矮了一點點而已,我們可以從以下的操作與圖形 當中看到 T 分布與常態分布之間的差異。
> curve(dnorm, from=-3, to=3, col="black")
> curve(dt(x, df=25), from=-3, to=3, add=T, ylab="T25", col="blue")
> curve(dt(x, df=10), from=-3, to=3, add=T, ylab="T10", col="red")
> curve(dt(x, df=3), from=-3, to=3, add=T, ylab="T3", col="green")
>
有了 T 分布,我們就可以用來檢定 sd 未知情況下的平均數了,以下是我們的操作過程。
> t.test(x)
One Sample t-test
data: x
t = 17.5128, df = 24, p-value = 3.562e-15
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
7.205820 9.131145
sample estimates:
mean of x
8.168483
上述操作中,我們用 T 分配來推估母體的平均值範圍,程式的輸出顯示其 95% 信賴區間是 (7.205820, 9.131145)。
事實上、t.test 所作的並不只是「估計信賴區間」而已,而是具有「檢定」某個假設可能程度的功能,因此才稱為 test。
在上述檢定中,我們檢定的「對立假設」(alternative hypothesis) 是 mu≠0 (true mean is not equal to 0) ,也就是 「虛無假設」是 mu=0 ,結果顯示虛無假設成立的「顯著性」只有 3.562e-15 ( $3.562*10^{-15}$ ) ,可以說是幾乎不可能。
這個結果是合理的,因為我們用來產生樣本的母體其實是 N(mean=8, sd=2) ,距離 0 實在太遠了。
如果我們將 mu 改設為 8 重新進行一次檢定,您將會看到檢定結果如下:
> t.test(x, mu=8)
One Sample t-test
data: x
t = 0.3612, df = 24, p-value = 0.7211
alternative hypothesis: true mean is not equal to 8
95 percent confidence interval:
7.205820 9.131145
sample estimates:
mean of x
8.168483
在採用 mu=8 所進行的檢定當中,我們看到「顯著性」變成了 p-value = 0.7211,這比起 mu=0 的 p-value = 3.562e-15 大太多了, 代表 mu=8 是有可能的,我們無法否決這樣的可能性。
另外、輸出報告中也顯示了自由度 df = 24,T 分布中所謂的自由度其實是樣本數減一 (25-1=24)。
註:那麼、上述 p-value=0.7211 的値是怎麼來的呢?這牽涉到雙尾檢定的問題,因為我們想檢定的對象是 $\mu=8$ ,這代表我們想要找 到一個 t 分布且自由度 df=24 的値,使其在截掉兩尾端面積的情況下,剩下的機率累計是 0.7211。如下操作所示:
> half = (1-0.7211)/2
> df1 = 24
> from=qt(half, df=df1)
> to=qt(1-half, df=df1)
> pt(to, df=df1)-pt(from, df=df1)
[1] 0.7211
檢定的概念
想必讀到這裡,一定有人在想:我搞不清楚你說的「對立假設」、「虛無假設」、「顯著性」是甚麼東西,讓我們補充如下。
根據某些樣本,推論統計可以進行實驗的檢定某個假設 H1 是否可能,其方法是透過否定對立假設 H0,看看 H0 是否不太可能發生。
- H1:稱為研究假設 (research hypothesis) 或對立假設 (alternhative hypothesis)
- H0:稱為虛無假設 (null hypothesis)
透過推論統計,我們可以檢查實驗結果是否具有顯著性 (假設檢定),也就是實驗的假設 H1 是否要被接受, 由於 H0 是H1 的對立假設 (不是 H0 就是 H1,也就是 H1 = not H0),因此一旦否決了 H0 就代表接受了 H1。
舉例而言,以上述的 mu = 0 的情況,其虛無假設 H0 與對立假設 H1 分別如下。
- H0: mu=0
- H1: mu≠0
在進行假設檢定的推論時,我們可能推論正確,也可能推論錯誤,以下是四種可能的推論情況。
| 決策 | H0 為真 | H1 為真 |
|---|---|---|
| 拒絕 H0 | 型 I 錯誤 (H0 為真卻拒絕 H0) | 正確決策 |
| 無法拒絕 H0 | 正確決策 | 型 II 錯誤 (H1 為真卻無法拒絕 H0) |
以實例來說,對於 mu 的情況,其推論決策如下表所示。
| 決策 | H0 : mu=0 為真 | H1 : mu ≠ 0 為真 |
|---|---|---|
| 拒絕 mu=0 | 型 I 錯誤 ( mu=0 卻被我們拒絕) | 正確決策 |
| 無法拒絕 mu=0 | 正確決策 | 型 II 錯誤 ( mu ≠ 0 卻無法拒絕 mu=0) |
當然我們會希望正確決策的機會越大越好,而錯誤決策的機會越小越好。假設檢定可以告訴我們各類型正確與錯誤決策的機率, 以便讓我們知道是否要接受 H1 而拒絕 H0。
在檢定的結果中,我們可以用幾個線索決定是否要拒絕虛無假設 H0,改承認對立假設 H1 ,其根據大致上可以從檢定報告的 兩個部分看出來,第一部分是從「信賴區間」中可以看出,第二部分是從顯著性 P 值當中看出。
在上述兩次的檢定當中,由於 mu=8 位於 95% 信賴區間 (7.205820 9.131145) 之內,因此虛無假設 mu=8 無法被拒絕,也就是 mu=8 是有可能且合理的,但是 mu=0 位於 95% 信賴區間 (7.205820 9.131145) 之外,因此是不太可能,而且應該被拒絕的, 也就是 mu ≠ 0 才是比較合理且可能的。
另外,也可以採用顯著性 (P 值, p-value) 的方式判別,所謂的 P 值就是樣本的不合理性,舉例而言,以上述的 mu=0 的情況, P 值就被定義為 $P(\bar{x} > 8.168483 | mu=0)$ 的機率值,由於 mu=0 的分布會產生這麼大的一組平均值的情況非常罕見, 機率只有 3.562e-15 ,因此我們可以很有信心的拒絕 H0:mu=0 這個虛無假設,改採 H1:mu ≠ 0 這個對立假設。
因此在上述兩次檢定中,由於 mu=8 的顯著性 (p-value) 為 $P(\bar{x} > 8.168483 | mu=8)=0.7211$ 算蠻大的, 所以無法被拒絕,也就是 mu=8 是有可能且合理的。
但是在 mu=0 的檢定中,p-value = 3.562e-15,已經小到不可思議的程度,因此該檢定結果強烈拒絕 mu=0 這樣的假設, 改為支持對立假設 mu ≠ 0 。
檢定的圖形
為了讓讀者更清楚的理解檢定的結果,我們找到了 R 軟體的一個套件,稱為 visualizationTools , 您可以透過 install.packages(“visualizationTools”) 這個指令安裝該套件,然後用像下列指令 顯示檢定的結果。
plot(t.test(x, mu=5))
以下是一個完整的檢定與圖形顯示過程:
> x = rnorm(25, mean=5.5, sd=2)
> t.test(x, mu=5)
One Sample t-test
data: x
t = 0.8254, df = 24, p-value = 0.4173
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
4.508086 6.147536
sample estimates:
mean of x
5.327811
> install.packages("visualizationTools")
--- Please select a CRAN mirror for use in this session ---
嘗試 URL 'http://cran.csie.ntu.edu.tw/bin/windows/contrib/3.0/visualizationTools_0.2.05.zip'
Content type 'application/zip' length 102524 bytes (100 Kb)
開啟了 URL
downloaded 100 Kb
package ‘visualizationTools’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\ccc\AppData\Local\Temp\RtmpyCqQmq\downloaded_packages
> library("visualizationTools")
> plot(t.test(x, mu=5))
>
上述指令所顯示的圖形如下所示:
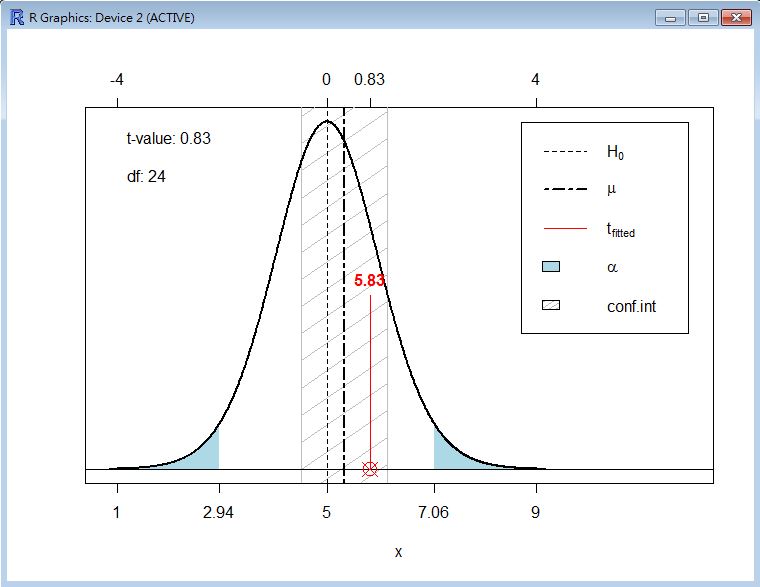
解讀:
在變異數未知情況下,以下的平均值 $\bar{X}$ 會服從自由度為 n-1 的 T 分布如下。
$\frac{\bar{X}-\mu}{S/\sqrt{n}} \sim T_{n-1}(\mu, S)$
如果從 $\mu$ 固定的角度來看,則 $\bar{X}$ 分布於以 $\mu$ 為中心點的 $T_{n-1}(\mu, S)$ 分布, 但若以 $\bar{X}$ 固定的角度反觀,則 $\mu$ 落在以 $\bar{X}$ 為中心的「信賴區間」內,與信賴區間 重疊的機率為 $1-\alpha/2$ 。
習題
習題一、以下 x 是某隨機樣本序列,請回答下列問題
x = c(46.26534, 49.30766, 53.79364, 53.18000, 48.97584, 51.92664, 44.58280, 62.26655, 54.52493, 55.08502, 56.78329, 45.00972, 46.99871, 43.88388, 52.63184, 53.15600, 48.39374, 51.07595, 47.36923, 52.09186, 46.54074, 54.46617, 47.87038, 42.94228, 48.69307)
- 請問母體平均值 mu 的 95% 信賴區間為何?
- 請問母體平均值 mu 的 98% 信賴區間為何?
- 請用 mu=50 檢定該平均值 (a) 請問該檢定的虛無假設為何? (b) 請問該檢定的對立假設為何? (c) 請問顯著性 p-value 是多少? (d) 請問您認為 mu=50 這個虛無假設是否應該被否決?為甚麼? (e) 請問您認為 mu 不等於 50 這個對立假設是否應該被接受?為甚麼?
習題二、請用下列方式產生樣本 x,然後回答下列問題
mu=runif(1, 0, 10)
sd1 = runif(1, 1,2)
x=rnorm(25, mean=mu, sd=sd1)
x
- 請問母體平均值 mu 的 95% 信賴區間為何?
- 請問母體平均值 mu 的 98% 信賴區間為何?
- 請用 mu=5 檢定該平均值 (a) 請問該檢定的虛無假設為何? (b) 請問該檢定的對立假設為何? (c) 請問顯著性 p-value 是多少? (d) 請問您認為 mu=5 這個虛無假設是否應該被否決?為甚麼? (e) 請問您認為 mu ≠ 5 這個對立假設是否應該被接受?為甚麼?
參考文獻
- 免費電子書 – 機率與統計 (使用 R 軟體) – http://ccckmit.wikidot.com/st:main
- 工程統計學:原則與應用(修訂版)(Milton 4/e), 作者:Milton, 譯者:吳榮彬, 年份:2008年 4版, ISBN:9789861574080