隨機變數
隨機變數簡介
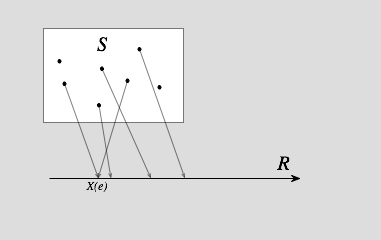
如果 X 指定給機率空間 S 中每一個事件 e 一個實數 X(e),同時針對每一個實數 r 都有一個事件集合 $A_r$ 與其相對應,其中 $A_r = {e:X(e) \le r}$,那麼 X 被稱作隨機變數。
隨機變數是機率理論當中非常重要的一個概念,但是卻也非常容易被誤解,因為隨機變數其實是一種函數,而非只是簡單的變數,以下是機變數的定義。
隨機變數 (Random Variable)
定義:隨機變數是以樣本空間 S 為定義域的實數值函數,可以寫為 X(s),其中 $s \in S, X(s) \in R$
換言之,隨機變數 X 是一個機率空間 (probability space) 中的函數, 可以寫為 $X(S) \rightarrow R$ ,該函數將 S 的某一子集合映射到實數領域 R。
舉例而言,投擲一個銅板時,可能出現正面或反面,此時的樣本空間 S = {正面、反面}。
假如這是一個公平的銅板,兩面的機率各為 1/2,那麼我們就可以寫為 P(正面) = 1/2, P(反面) = 1/2。
但是在這樣的描述當中,並沒有函數的慨念,因此不符合隨機變數的定義。
如果我們用一個函數 X,代表銅板正面出現的次數,那麼 X 會將 {正面、反面} 映設到 {1,0} ,這樣的函數才符合隨機變數的定義。我們可以寫為 $X(S) \rightarrow R$,其中的樣本空間 S={正面、反面},且 X(正面)=1,X(反面) = 0。
為何要這麼麻煩呢?為何我們不直接指定樣本空間中每一元素的機率就好了呢?
原因之一是,採用隨機變數概念的描述,才能將函數引入到機率模型中,這樣也才能更方便的描述一系列的隨機試驗。
舉例而言,假如我們投擲兩個銅版,出現正面的個數為一個隨機變數,假如這個隨機變數稱為 X2,那麼 X2 的定義域 (樣本空間) 就是 S2={正正、正反、反正、反反},那麼隨機變數 X2 就會將 S2 空間中的元素映射到 {2, 1, 0} 這些實數值上,如下所示:
X2(正正) = 2
X2(正反) = 1
X2(反正) = 1
X2(反反) = 0
這樣我們就可以用「機率密度函數」來描述各個事件出現的機率,例如用 P[X2=2] 代表出現兩次正面的機率,P[X2=1] 代表出現一次正面的機率,而P[X2=0] 代表沒有出現正面的機率。
範例:
隨機擲兩個骰子,整個事件空間可以由 36 個元素組成:
$S = \lbrace ( i, j ) | i=1, \ldots, 6,; j=1, \ldots,6 \rbrace$
這裡可以構成多個隨機變數,比如隨機變數 X ( 獲得的兩個骰子的點數和 ) 或者隨機變數 Y ( 獲得的兩個骰子的點數差),隨機變數 X 可以有 11 個整數值,而隨機變數 Y 只有 6 個。
$X ( i, j ) := i+j , x=2,3,\ldots,12$ ;
$Y ( i, j ) := \mid i-j \mid , y=0,1,2,3,4,5.$ ;
在此,我們引入了一個新的概念,稱為「機率密度函數」,讓我們更仔細的看看這個概念的意義。
習題 1:
問題: 請定義擲茭(博杯)的隨機變數
說明:
(a) 有杯映射到 1,沒杯映射到 0
(b) 樣本空間為 {正正、正反、反正、反反}
(c) { 正反、反正} 稱為有杯
解答:
X({正正}) = 0
X({正反}) = 1
X({反正}) = 1
X({反反}) = 0
補充:假如博杯正面積率為 0.6,反面機率為 0.4,而且兩個杯之間互相獨立,那麼假如根據機率公理第三條,可以算出:
P({正正}) = P(正) * P(正) = 0.6*0.6 = 0.36
P({正反}) = P(正) * P(反) = 0.6*0.4 = 0.24
P({反正}) = P(反) * P(正) = 0.4*0.6 = 0.24
P({反反}) = P(反) * P(反) = 0.4*0.4 = 0.16
所以
P(X=1) = P({正反, 反正}) = P({正反}) + P({反正}) = 0.24 + 0.24 = 0.48
P(X=0) = P({正正, 反反}) = P({正正}) + P({反反}) = 0.36 + 0.16 = 0.52
習題 2:
問題: 假如現在從你身上抽一滴血,請回答下列兩個問題。
- 請定義一個隨機變數 X 代表那滴血中的白血球數量。
提示: 樣本空間 S = 此時此刻你身上的所有白血球 = {w1,w2,……,wn}
- 請算出一滴血液中有三顆白血球的機率,假設該滴血液占你總血量的 1/1000。
解答 1:
X(A) = |A|
說明:
A 是一個事件,也就是白血球的樣本空間 S 的子集合,例如: A = {w1, w5, w9}
|A| 代表 A 集合的大小,也就是元素個數,舉例而言:
如果 A = {w1, w5, w9} ,那麼 |A| = 3
如果 B = {w2, w8},那麼 |B| = 2
如果 C = {},那麼 |C| = 0
如果 D = S,那麼 |D| = n
解答 2:
P(X=3) = P({A | X(A) = 3}) = P({{w1, w2, w3}) + P({w1, w2, w4}) + ……
假如任一顆白血球被抽到的機率等於該滴血液佔全身血液的比率,由於該滴血液佔總血量的 1/1000,所以給顆白血球被抽到的機率為 1/1000。
而且假設這些白血球沒有智慧,也不會聚合在一起,因此相互之間獨立,那麼由於每顆白血球被抽到的機率為 1/1000,因此 P(w1) = P(w2) = …. P(wn) = 1/1000。
那麼初步想法是 P(w1w3) = P(w1) * P(w3) = 1/1000 * 1/1000 。
但是上述的想法有個小問題,那就是該情況代表其它白血球都沒被抽到,因此所謂的 P(w1w3) 真正的意思應該是
$P(w_1 \bar{w_2} w_3 \bar{w_4} …. \bar{w_n}) = (\frac{1}{1000})^2 (\frac{999}{1000})^{n-2}$
所以 P(X=3) 應該算法如下:
$P(X=3) = P({A| X(A) = 3}) = (\frac{1}{1000})^3 (\frac{999}{1000})^{n-3} {n \choose 3}$
推而廣之,P(X=k) 的機率之算法如下:
$P(X=k) = P({A| X(A) = k}) = (\frac{1}{1000})^k (\frac{999}{1000})^{n-k} {n \choose k}$
事實上,這個題目的機率分布就是下一章的二項分布,如下所示:
$P(X=k) = {n \choose k} p^k (1-p)^{n-k}$
而且、當 n 趨近於無限大時,這個分布將會趨近於布瓦松分布,如下所示:
$P(X=k) = \lambda^k e^{-\lambda}/k!$
其中的 λ 之意義為,在單位時間 (或單位面積、體積) 內,事件的出現次數平均為 λ 次。
離散與連續
如果隨機變數 X 的取值是有限的或者是可數無窮盡的值,則稱 X 為離散隨機變數,如下所示:
$X = \lbrace x_1, x_2, x_3, \ldots, \rbrace$
如果 X 由全部實數或者由一部分區間組成,則稱 X 為連續隨機變數,連續隨機變數的值是不可數及無窮盡的。
$X = \lbrace x | a\le x \le b \rbrace$
例如:擲骰子和丟銅版,都是離散型的隨機變數。而常態分布或均等分布,則是連續型的隨機變數之分布。
機率密度函數 (Probabilistic Density Function)
機率密度函數 (Probabilistic Density Function, PDF)
定義:機率密度函數則是一個符合機率公理的的函數 P,當我們寫 P[X=x] 時,意味著 x 是一個特定實數,其機率定義如下:
$P[X=x] = P(S_x) = P({s:X(s)=x}) = \sum_{s \in S_x} P(s)$
其中的 $S_x$ 乃是一個 S 的子集合,定義為 $S_x = {s:X(s)=x}$ 。
舉例而言,P[X=2] 代表 $P({s \in S: X(s)=2})$ 的機率。
讓我們來看看更多的機率密度函數的範例。
範例 1:
在投擲銅板的機率過程中,其樣本空間 S={正, 反} ,
而其中一個常見的隨機變數 X ,是用來計算銅板的正面數量,
也就是 X(正) =1, X(反) = 0。
此時,P[X=1] = P({正}) = 0.5,而 P[X=0] = P({反}) = 0.5
範例 2:
在投擲兩個銅板的機率過程中,其樣本空間 S={正正, 正反, 反正, 反反} ,
而其中一個常見的隨機變數 X ,是用來計算銅板的正面數量,
也就是 X(正正) =2, X(正反) = X(反正) = 1, X(反反) = 0。
P[X=2] = P({正正}) = 0.25 P[X=1] = P({正反,反正}) = 0.5 P[X=0] = P({反反}) = 0.25
範例 3:
在投擲骰子的機率過程中,其樣本空間 S={1點,2點,3點,4點,5點,6點},
而其中一個常見的隨機變數 X ,是用來計算點數的,
也就是 X(1點) =1, X(2點) = 2, … X(6點) = 6。
此時,P[X=1] = P[X=2] = … = P[X=6] = 1/6。
範例 4:
在投擲骰子的機率過程中,其樣本空間 S={1點,2點,3點,4點,5點,6點},
而其中一個不常見的隨機變數 Y ,是用來辨認偶數點的,
也就是 Y(1點) =0, Y(2點) = 1, Y(3點) = 0, Y(4點) = 1, Y(5點) = 0, Y(6點) = 1。
此時,P[Y=1] = P[Y=0]= 1/2。
累加分配函數 (Cumulative Distribution Function)
有了上述的「隨機變數」與「機率密度函數」之後,我們就可以很容易的定義「累加分配函數」這種在「實數值」上的概念了。
累加分配函數 (Cumulative Distribution Function, CDF)
定義:累加分配函數 F(x) 代表所有小於 x 的機率密度函數之累加值 $F(x) = P[X \le x]$
離散情況:$F(x_0) = \sum_{x \le x_0} P[X=x] = \sum_{x \le x_0} P(x)$
連續情況:$F(x_0) = \int_{-\infty}^{x_0} P[X=x] dx = \int_{-\infty}^{x_0} f(x) dx$
為了方便起見,我們經常會將 P[X=1] 簡寫成 P(1) 或 f(1),P[X=x] 簡寫成 P(x) 或 f(x)。 所以上面公式中的 P(x) 是離散情況中機率密度函數 P[X=x] 的簡寫,而 f(x) 是連續情況中 P[X=x] 的簡寫。
隨機變數的代數運算
在單一個樣本空間 S 中,可以有很多不同的隨機變數 X, Y, … ,因為將 S 映射到 R 的函數有很多,例如:
X(s) 其中 $s \in S, X(s) \in R$
Y(s) 其中 $s \in S, Y(s) \in R$
…
在機率統計中,我們經常看到隨機變數可以像數值一樣進行 +, -, * 等運算。舉例而言,假如 X, Y 均為隨機變數,那麼 「X+Y」, 「X-Y」, 「X*Y」 等都是隨機變數。
但是在前文中,我們看到了隨機變數其實被定義為一個「實數值函數」$X(S) \to R$,那麼這些 +, -, * 等運算就是在函數上所進行的運算,這些運算的函意到底是甚麼呢?
3X 的意義
隨機變數 3X 代表的是一個函數 Z=3X,其中 Z 函數對每一個元素 s 的映射值均為 X 的 3 倍,也就是:
Z(s) = 3 * X(s)
範例:
問題:令 X 為擲骰子點數的隨機變數,也就是 X(k點)=k (k=1..6),那麼隨機變數 3X 代表的是 Z(k點)=3*X(k點)=3k 這個函數。
根據這樣的表示方法,如果 Z = 3X,那麼請計算下列機率值。
- 請問 P[Z=3] = ?, (答案為1/6)
- 請問 P[Z=1] = ?, (答案為0)
- 請問 P[Z=18] = ?, (答案為1/6)
- 請問 P[Z=5] = ?, (答案為0)
範例:
問題:令 X 為丟銅板所得正面次數的隨機變數,也就是 X(正)=1, X(反)=0,那麼隨機變數 Z=3X 代表的是 Z(正)=3,Z(反)=0 這個函數。
X+Y 的意義
隨機變數 X+Y 代表的是一個函數 Z=X+Y,其中 Z 函數對每一個元素 s 的映射值均為 X + Y 的映射值總和,也就是:Z(s) = X(s)+Y(s)
範例:
令 X, Y 均為為擲骰子點數的隨機變數,也就是 X(k點)=Y(k點)=k (k=1..6),那麼 X+Y 代表的是隨機變數 Z(k點)=2k 這個隨機變數。
範例:
問題:令 X 為擲骰子點數的隨機變數,Y 為丟銅板所得正面次數的隨機變數,那麼 X+Y 這個隨機變數代表甚麼意義呢?
解答:這兩個隨機變數的定義域不同,因此不能相加,但是若我們將定義域擴展為聯合分布,那麼就可以相加。
在這個範例中,X 與 Y 兩者的定義域 SX, SY 並不相同,因此必須用聯合隨機分布的概念,也就是同時投擲一顆骰子與一個銅板,才能有效說明 X+Y 的意義。
對於定義域不同的兩個隨機變數而言,其樣本空間可用兩者的「笛卡兒」乘積代表,也就是 SX = {1點,…., 6點} , 而 SY = {正, 反}。
此時 X+Y 所在的樣本空間,必須解釋為 {1點,…., 6點} 與 {正, 反} 兩者的笛卡兒乘積,總共有 12 種可能,聯合分布的樣本空間 S 如下所示。
S = $(S_X, S_Y)$ = { (1點, 正), (1點,反), (2點, 正), (2點,反), ….(6點, 正), (6點,反)}
因此,Z = X+Y 所代表的隨機變數,其實是一個 Z 函數,該函數將 $(S_X, S_Y)$ 映射到實數 R 中,其中的 X 作用在 $S_X$ 上,而 Y 作用在 $S_Y$ 上,也就是: Z(s) = Z(x, y) = X(x)+Y(y)
所以,P(Z=2) 也可以寫成 P(X+Y = 2) ,也就是 P({(1點, 正), (2點,反)}),因此 P(Z=2) 的機率為 2/12 = 1/6。
X Y 的意義
隨機變數 X Y 代表的是一個函數 Z=X Y,其中 Z 函數對每一個元素 s 的映射值均為 X Y 的映射值乘積,也就是:
Z(s) = X(s) Y(s)
範例:
問題:令 X 為擲骰子點數的隨機變數,Y 為丟銅板所得正面次數的隨機變數,那麼 X Y 這個隨機變數代表甚麼意義呢?
解答:這兩個隨機變數的定義域不同,因此不能相加,但是若我們將定義域擴展為聯合分布,那麼就可以相加。
同上一個範例,X 與 Y 兩者的定義域 $(S_X, S_Y)$ 並不相同,樣本空間仍然用其「笛卡兒」乘積代表。
S = $(S_X, S_Y)$ = { (1點, 正), (1點,反), (2點, 正), (2點,反), ….(6點, 正), (6點,反)}
因此,Z = X Y 所代表的隨機變數,其實是一個 Z 函數,該函數將 $(S_X, S_Y)$ 映射到實數 R 中,其中的 X 作用在 $S_X$ 上,而 Y 作用在 $S_Y$ 上。
所以,P(Z=2) 也可以寫成 P(X Y = 2) ,也就是 P({(2點, 正)}) ,因此 P(Z=2) 的機率為 1/12。
X^k 的意義
隨機變數 $X^k$ 代表的是一個函數 $Z=X^k$,其中 Z 函數對每一個元素 s 的映射值均為 X(s) 的 k 次方,也就是: $Z(s) = X^k(s)$
範例:X 為投擲 1 顆骰子點數的隨機變數,且定義 $Z = X^2$,請問隨機變數 P(Z=4) 的機率為何?
解答:
$Z(s)=4=X^2(s)=X(s) * X(s) \quad \rightarrow \quad X(s) = 2$
所以 P(Z=4) 相當於 P(X=2) = P({2點}) = 1/6
但必須注意的是 Z 的定義域雖仍然為 ({1點,…., 6點}),但是值域卻為 1,4,9,16,25,36。
結語
隨機變數 X, Y, Z, … 乃是一種作用於樣本空間 S 的實函數,此種函數會將樣本點映射到實數中,例如: $X(S) \to R$ 代表函數 X 將樣本空間中的元素 s 映射到某個實數值 x。
利用隨機變數映射完成之後,就可以比較大小,因此可以計算「機率密度函數」與「累加分配函數」,這樣就能利用加總或積分去計算某個區間內的機率,讓機率模型得以進行數學性的運算。
我想這是為甚麼數學家要將隨機變數定義成實函數的原因之一吧!