機率分布 (離散型)
簡介
在程式設計領域,「設計模式」是一些經常被使用到的物件樣式,而在數學領域,也同樣存在著某些「常見模式」,在機率統計領域,這些「常見模式」就是機率分布。
機率分布可以分為「離散型」與「連續型」兩類,以下是一些常見的離散型機率分布。
| 離散機率模型 | 密度函數 | R 函數名稱 | 說明 |
|---|---|---|---|
| 二項分布 | ${n \choose x} p^x (1-p)^{n-x}$ | binom(n:size, p:prob) | n:樣本數, p:正面機率, n 次試驗中有 x 個成功的機率 |
| 多項分布 | $\frac{n!}{x_1!…x_k!} p_1^{x_1}…p_k^{x_k}$ | multinom(n:size, p(1..k):prob) | n:樣本數, p[1..n]:各項的機率 |
| 負二項分布 | ${x-1 \choose r-1} (1-p)^{x-r} p^r$ | nbinom(size, prob) | x:樣本數, , p:正面機率, 要得到第 r 次成功所需要的試驗次數 |
| 幾何分布 | $(1-p)^{x-1} p$ | geom(p:prob) | p: 成功機率, 第一次成功所需要的試驗次數 |
| 超幾何分布 | $\frac{ { r \choose x} {N-r \choose n-x} }{N \choose n}$ | hyper(N:m,n:n,r:k) | m:白球數量, n:黑球數量, k:抽出球數, 同二項分布,但取樣後不放回 |
| 布瓦松分布 | $\frac{e^{-\lambda s} {\lambda s}^x}{x!}$ | pois(lambda) | k:期望值, $\lambda = \frac{k}{s}$, 在 s 時間內,事件出現平均 k 次 |
二項分布 (Binomial distribution)
分布公式:$f(x) = {n \choose x} p^x (1-p)^{n-x}$
意義:dbinom(x; n, p):在 n 次柏努力試驗中有 x 次成功的機率 (已知單次試驗成功機率為 p)。
R 的公式:dbinom(x; n, p) = p(x) = choose(n,x) p^x (1-p)^(n-x)
- R 函數:binom(size=n:樣本數, prob=p:成功機率)
- http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Binomial.html
二項定理: $(a+b)^n = \sum^{n}_{k=0} {n \choose k} a^k b^{n-k}$
特性
- $E(X) = \mu = np$
- $Var(X) = \sigma^2 = np (1-p) = npq$
動差生成函數: $m_x(t) = ((1-p)+pe^t)^n = (q+pe^t)^n$
R 程式範例:二項分布曲線圖
> n=10; p=0.3; k=seq(0,n)
> plot(k, dbinom(k,n,p), type='h', main='dbinom(0:20, n=10, p=0.3)', xlab='k')
>
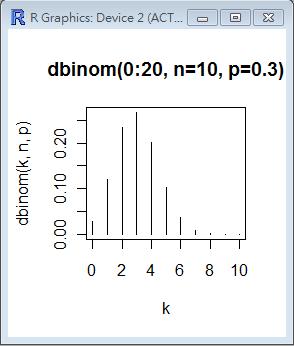
R 程式範例:(定理) 常態分配可用來逼近二項分布
假如 n 夠大的話,通常只要 n*min(p, 1-p) > 5 就可以採用下列逼近方式
$binom(n, p) \rightarrow norm(np, np(1-p))$
原始程式:
op=par(mfrow=c(2,2))
n=3; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=3, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=5; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=5, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=10; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=10, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=100; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=100, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
輸出圖形:
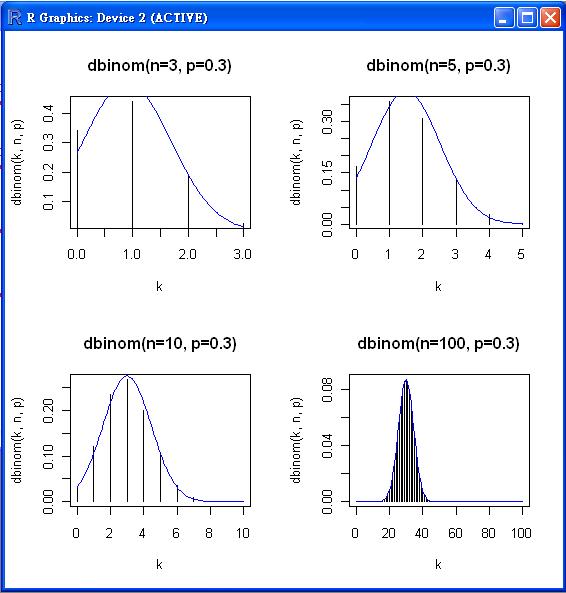
R 程式範例:二項分布統計圖
> x = rbinom(100000, 100, 0.8)
> hist(x, nclas=max(x)-min(x)+1)
>
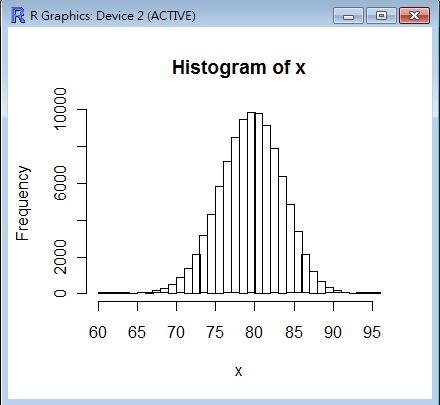
R 程式範例四:白努力試驗
> y <- rbinom(50, 25, .4)
> m1 <- mean(y)
> m2 <- sum(y) / 25
> y
[1] 12 9 9 9 12 11 10 11 5 7 8 7 16 6 12 13 9 12 9 13 7 12 15 8
[25] 9 7 10 4 10 10 9 10 13 8 10 14 8 11 11 10 10 9 7 13 5 5 11 13
[49] 9 8
> m1
[1] 9.72
> m2
[1] 19.44
> m3 <- sum ( (y-m1)^2 ) / 50
> m3
[1] 6.8816
>
說明: y 中的每個數字,代表模擬投擲 25 次白努力試驗後,成功的次數有幾次。因此 rbinom(50, 25, .4) 總共進行了 50*25 次白努力試驗。
參考文獻
- Distributions in the stats package – http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Distributions.html
- Wikipedia:二項分佈 – http://zh.wikipedia.org/wiki/%E4%BA%8C%E9%A0%85%E5%88%86%E4%BD%88
- Wikipedia:Binomial_distribution – http://en.wikipedia.org/wiki/Binomial_distribution
負二項分布 (Netative binomial distribution)
公式:$f(x) = {x-1 \choose r-1} (1-p)^{x-r} p^r$
範圍:r=1,2,3,…. ; x= r, r+1, r+2, ….
意義:要得到第 r 次成功所需要的試驗次數 x;
R 函數: nbinom(size, prob) ; r:size:成功數, p:prob:成功機率
特性
- $E(X) = r/p$
- $Var(X) = r (1-p)/p^2 = r q/p^2$
動差生成函數:$m_x(t) = \frac{(pe^t)^r}{(1-(1-p) e^t)^r} = \frac{(p e^t)^r}{(1-q e^t)^r}$
R 程式範例:負二項分布曲線圖
> n=20; p=0.4; k=seq(0,50)
> plot(k, dnbinom(k,n,p), type='h', main='dnbinom(k,n=20,p=0.4)', xlab='k')
>
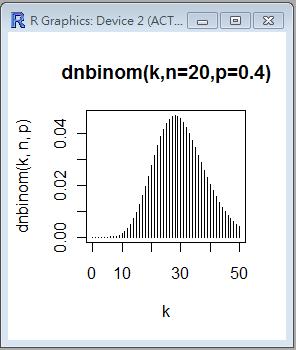
> x = rnbinom(100000, 100, 0.8)
> hist(x, nclass=max(x)-min(x)+1)
>
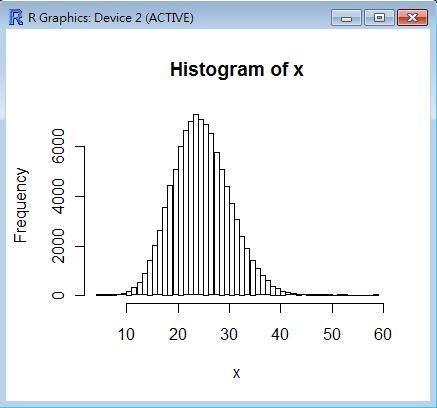
R 程式範例 (進階)
require(graphics)
x <- 0:11
dnbinom(x, size = 1, prob = 1/2) * 2^(1 + x) # == 1
126 / dnbinom(0:8, size = 2, prob = 1/2) #- theoretically integer
## Cumulative ('p') = Sum of discrete prob.s ('d'); Relative error :
summary(1 - cumsum(dnbinom(x, size = 2, prob = 1/2)) /
pnbinom(x, size = 2, prob = 1/2))
x <- 0:15
size <- (1:20)/4
persp(x,size, dnb <- outer(x, size, function(x,s) dnbinom(x,s, prob= 0.4)),
xlab = "x", ylab = "s", zlab="density", theta = 150)
title(tit <- "negative binomial density(x,s, pr = 0.4) vs. x & s")
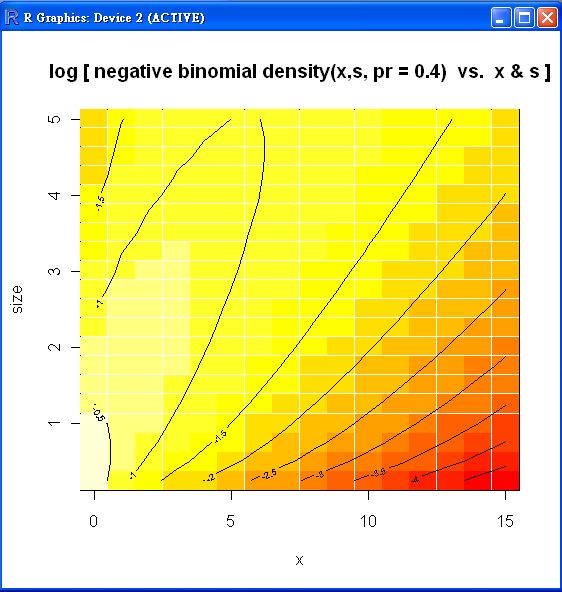
image (x,size, log10(dnb), main= paste("log [",tit,"]"))
contour(x,size, log10(dnb),add=TRUE)
## Alternative parametrization
x1 <- rnbinom(500, mu = 4, size = 1)
x2 <- rnbinom(500, mu = 4, size = 10)
x3 <- rnbinom(500, mu = 4, size = 100)
h1 <- hist(x1, breaks = 20, plot = FALSE)
h2 <- hist(x2, breaks = h1$breaks, plot = FALSE)
h3 <- hist(x3, breaks = h1$breaks, plot = FALSE)
barplot(rbind(h1$counts, h2$counts, h3$counts),
beside = TRUE, col = c("red","blue","cyan"),
names.arg = round(h1$breaks[-length(h1$breaks)]))
執行結果:
> require(graphics)
> x <- 0:11
> dnbinom(x, size = 1, prob = 1/2) * 2^(1 + x) # == 1
[1] 1 1 1 1 1 1 1 1 1 1 1 1
> 126 / dnbinom(0:8, size = 2, prob = 1/2) #- theoretically integer
[1] 504.0 504.0 672.0 1008.0 1612.8 2688.0 4608.0 8064.0 14336.0
>
> ## Cumulative ('p') = Sum of discrete prob.s ('d'); Relative error :
> summary(1 - cumsum(dnbinom(x, size = 2, prob = 1/2)) /
+ pnbinom(x, size = 2, prob = 1/2))
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.22e-16 -2.22e-16 -2.22e-16 -1.48e-16 0.00e+00 0.00e+00
>
> x <- 0:15
> size <- (1:20)/4
> persp(x,size, dnb <- outer(x, size, function(x,s) dnbinom(x,s, prob= 0.4)),
+ xlab = "x", ylab = "s", zlab="density", theta = 150)
> title(tit <- "negative binomial density(x,s, pr = 0.4) vs. x & s")
>
> image (x,size, log10(dnb), main= paste("log [",tit,"]"))
> contour(x,size, log10(dnb),add=TRUE)
>
> ## Alternative parametrization
> x1 <- rnbinom(500, mu = 4, size = 1)
> x2 <- rnbinom(500, mu = 4, size = 10)
> x3 <- rnbinom(500, mu = 4, size = 100)
> h1 <- hist(x1, breaks = 20, plot = FALSE)
> h2 <- hist(x2, breaks = h1$breaks, plot = FALSE)
> h3 <- hist(x3, breaks = h1$breaks, plot = FALSE)
> barplot(rbind(h1$counts, h2$counts, h3$counts),
+ beside = TRUE, col = c("red","blue","cyan"),
+ names.arg = round(h1$breaks[-length(h1$breaks)]))
繪圖結果:
參考文獻
多項分布 (Multinomial Distribution)
分布公式:$\frac{n!}{x_1!…x_k!} p_1^{x_1} p_2^{x_2}…p_k^{x_k}$
意義:n 次試驗中各種情況分別出現 x1, x2, …, xk 次的機率
範圍: $x_1, x_2, …, x_k=0,1,2,…,n ; 0<p[i]<1$
R 函數:multinom(size, prob) ; n:size:樣本數, p:prob:各種情況的機率
R 函數範例:
rmultinom(10, size = 12, prob=c(0.1,0.2,0.8))
pr <- c(1,3,6,10) # normalization not necessary for generation
rmultinom(10, 20, prob = pr)
## all possible outcomes of Multinom(N = 3, K = 3)
X <- t(as.matrix(expand.grid(0:3, 0:3))); X <- X[, colSums(X) <= 3]
X <- rbind(X, 3:3 - colSums(X)); dimnames(X) <- list(letters[1:3], NULL)
X
round(apply(X, 2, function(x) dmultinom(x, prob = c(1,2,5))), 3)
執行結果:
> rmultinom(10, size = 12, prob=c(0.1,0.2,0.8))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 0 2 0 1 1 0 2
[2,] 1 2 3 0 3 0 2 1 1 2
[3,] 10 9 8 12 7 12 9 10 11 8
>
> pr <- c(1,3,6,10) # normalization not necessary for generation
> rmultinom(10, 20, prob = pr)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 2 2 1 1 2 1 1 2
[2,] 2 2 2 2 6 7 3 5 4 4
[3,] 9 4 8 4 8 8 4 7 3 6
[4,] 8 13 8 12 5 4 11 7 12 8
>
> ## all possible outcomes of Multinom(N = 3, K = 3)
> X <- t(as.matrix(expand.grid(0:3, 0:3))); X <- X[, colSums(X) <= 3]
> X <- rbind(X, 3:3 - colSums(X)); dimnames(X) <- list(letters[1:3], NULL)
> X
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
a 0 1 2 3 0 1 2 0 1 0
b 0 0 0 0 1 1 1 2 2 3
c 3 2 1 0 2 1 0 1 0 0
> round(apply(X, 2, function(x) dmultinom(x, prob = c(1,2,5))), 3)
[1] 0.244 0.146 0.029 0.002 0.293 0.117 0.012 0.117 0.023 0.016
>
幾何分布 (Geometric distribution)
$P(X=x) = (1-p)^{x-1} p = q^{x-1} p$
範圍:r=1,2,3,…. ; x= r, r+1, r+2, ….
意義:第一次成功所需要的試驗次數。
R 函數: geom(prob) ; p:prob:成功機率, x-1:size:失敗次數, q:失敗機率
- R 的公式:$p(x) = p (1-p)^x$
- R 當中的 x 代表失敗次數,而非第一次成功的次數,因此 R 當中的 x 相當於上式中的 (x-1)
- http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Geometric.html
特性:
- $E = 1/p$
- $Var(X) = \frac{(1-p)}{p^2} = \frac{q}{p^2}$
動差生成函數:$m_x(t) = \frac{p e^t}{1-(1-p) e^t}= \frac{p e^t}{1-q e^t}$
R 程式範例:曲線圖
p=0.7; k=seq(0,10)
plot(k, dgeom(k, p), type='h', main='dgeom(p=0.5)', xlab='k')
R 程式範例:
qgeom((1:9)/10, prob = .2)
Ni <- rgeom(20, prob = 1/4); table(factor(Ni, 0:max(Ni)))
執行結果:
> qgeom((1:9)/10, prob = .2)
[1] 0 0 1 2 3 4 5 7 10
> Ni <- rgeom(20, prob = 1/4); table(factor(Ni, 0:max(Ni)))
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 3 2 0 3 1 0 0 0 1 0 0 0 0 0 0 1
>
參考
超幾何分布 (Hypergeometric distribution)
$f(x) = \frac{ {r \choose x} {N-r \choose{n-x} } }{N \choose n}$
意義:N 個球中有白球有 r 個,黑球 N-r 個,取出 n 個球,其中有 x 個白球的機率; (取後不放回)
R 函數: hyper(m,n,k) = choose(m, x) choose(n, k-x) / choose(m+n, k)
- R 函數的意義:m+n 個球中有白球有 m 個,黑球 n 個,取出 k 個球,其中有 x 個白球的機率; (取後不放回)
- R 的網址:http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Hypergeometric.html
- 課本與 R 之間對應公式:N=>m+n; n=>k; r=>m
- R 的公式:$P(X=x; m, n, k) = \frac{ {m \choose x} {n \choose{k-x} } }{ {m+n} \choose k}$
特性
- $E = k (\frac{m}{m+n})$
- $Var(X) = k (\frac{n}{m+n}) (\frac{m}{m+n}) (\frac{m+n-k}{m+n-1})$
動差生成函數:$m_x(t) = ???$
R 程式範例:曲線圖
m=10; n=5; k=8
x=seq(0,10)
plot(x, dhyper(x, m, n, k), type='h', main='dhyper(m=10,n=5,k=8)', xlab='x')
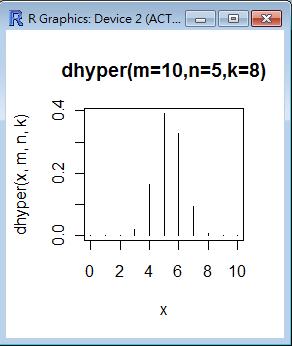
R 程式範例:
m <- 10; n <- 7; k <- 8
x <- 0:(k+1)
rbind(phyper(x, m, n, k), dhyper(x, m, n, k))
all(phyper(x, m, n, k) == cumsum(dhyper(x, m, n, k)))# FALSE
## but error is very small:
signif(phyper(x, m, n, k) - cumsum(dhyper(x, m, n, k)), digits=3)
執行結果:
> m <- 10; n <- 7; k <- 8
> x <- 0:(k+1)
> rbind(phyper(x, m, n, k), dhyper(x, m, n, k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 0 0.0004113534 0.01336898 0.117030 0.4193747 0.7821884 0.9635952
[2,] 0 0.0004113534 0.01295763 0.103661 0.3023447 0.3628137 0.1814068
[,8] [,9] [,10]
[1,] 0.99814891 1.00000000 1
[2,] 0.03455368 0.00185109 0
> all(phyper(x, m, n, k) == cumsum(dhyper(x, m, n, k)))# FALSE
[1] FALSE
> ## but error is very small:
> signif(phyper(x, m, n, k) - cumsum(dhyper(x, m, n, k)), digits=3)
[1] 0.00e+00 0.00e+00 1.73e-18 0.00e+00 -5.55e-17 1.11e-16 2.22e-16
[8] 2.22e-16 2.22e-16 2.22e-16
>
參考文獻
布瓦松分布 (Poisson distribution)
意義:在單位時間內,事件出現平均 λ 次的機率分布。
公式:$f(x) = \frac{e^{-k} k^x}{x!}$
R 的公式: $p(x) = \lambda^x e^{-\lambda}/x!$
R 函數:pois(λ:事件平均出現次數)
變數意義:$k = \lambda$
特性:
布瓦松分布可以與泰勒展開式中的 Maclaurin 級數對映起來,所謂的 Maclaurin 級數就是泰勒展開式在 0 點的展開式。
If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
$e^x = 1+x+x^2/2!+x^3/3!+ … + x^k/k! + ….$
布瓦松分配的公式來源
布瓦松分配可視為二項分配的極限形式,當 binom(n, p) 當中 n 趨近於無限大,而 p 非常小的時候,就會趨近布瓦松分配。
關鍵公式:$\lim_{n\to\infty}\left(1-{\lambda \over n}\right)^n=e^{-\lambda}$
證明過程:
$\lim_{n\to\infty} P(X_n=k) = \lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k}=\lim_{n\to\infty} {n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}$
$=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}{A_n}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}{\to\exp\left(-\lambda\right)}$ $\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}$
$=\left[ \lim_{n\to\infty} A_n \right] \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\to\left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)$
其中的 An 趨近於 1 ,證明如下:
$A_n= \frac{n!}{n^k\left(n-k\right)!}= \frac{n\cdot (n-1)\cdots \big(n-(k-1)\big)}{n^k}=1\cdot(1-\frac{1}{n})\cdots(1-\frac{k-1}{n})\to 1\cdot 1\cdots 1 = 1$
期望值與變異數
- $E(X) = k = \lambda$
- $Var(X) = k = \lambda$
動差生成函數:$m_x(t) = e^{k (e^t-1) } = e^{\lambda (e^t-1) }$
R 程式範例:曲線圖
lambda=5.0; k=seq(0,20);
plot(k, dpois(k, lambda), type='h', main='dpois(lambda=4.0)', xlab='k')
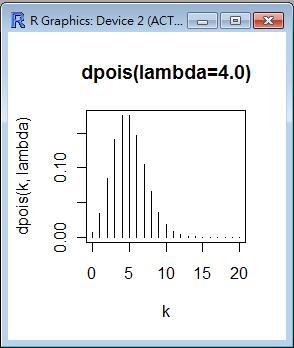
R 程式範例:
require(graphics)
-log(dpois(0:7, lambda=1) * gamma(1+ 0:7)) # == 1
Ni <- rpois(50, lambda = 4); table(factor(Ni, 0:max(Ni)))
1 - ppois(10*(15:25), lambda=100) # becomes 0 (cancellation)
ppois(10*(15:25), lambda=100, lower.tail=FALSE) # no cancellation
par(mfrow = c(2, 1))
x <- seq(-0.01, 5, 0.01)
plot(x, ppois(x, 1), type="s", ylab="F(x)", main="Poisson(1) CDF")
plot(x, pbinom(x, 100, 0.01),type="s", ylab="F(x)",
main="Binomial(100, 0.01) CDF")
執行結果:
> require(graphics)
>
> -log(dpois(0:7, lambda=1) * gamma(1+ 0:7)) # == 1
[1] 1 1 1 1 1 1 1 1
> Ni <- rpois(50, lambda = 4); table(factor(Ni, 0:max(Ni)))
0 1 2 3 4 5 6 7 8
1 3 6 8 11 11 4 3 3
>
> 1 - ppois(10*(15:25), lambda=100) # becomes 0 (cancellation)
[1] 1.233094e-06 1.261664e-08 7.085799e-11 2.252643e-13 4.440892e-16
[6] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[11] 0.000000e+00
> ppois(10*(15:25), lambda=100, lower.tail=FALSE) # no cancellation
[1] 1.233094e-06 1.261664e-08 7.085800e-11 2.253110e-13 4.174239e-16
[6] 4.626179e-19 3.142097e-22 1.337219e-25 3.639328e-29 6.453883e-33
[11] 7.587807e-37
>
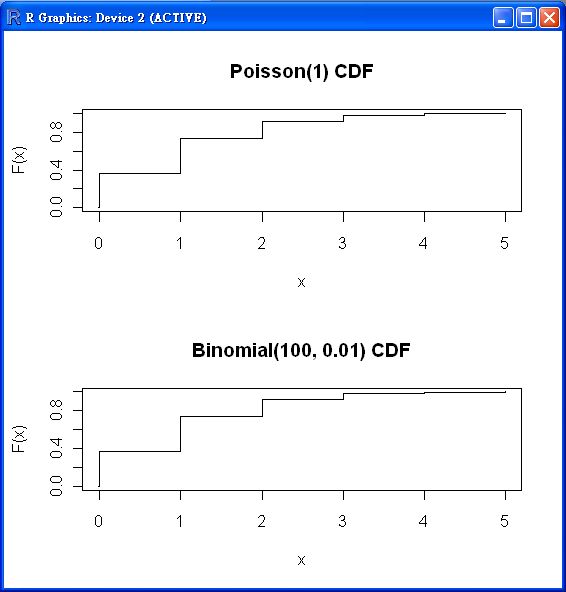
> par(mfrow = c(2, 1))
> x <- seq(-0.01, 5, 0.01)
> plot(x, ppois(x, 1), type="s", ylab="F(x)", main="Poisson(1) CDF")
> plot(x, pbinom(x, 100, 0.01),type="s", ylab="F(x)",
+ main="Binomial(100, 0.01) CDF")
>
參考文獻
二項分布 (Binomial distribution)
伯努力試驗
伯努利試驗(Bernoulli trial) 一種只有兩種可能結果的隨機試驗,可以用下列機率分布描述:
$Pr[X=1] = p \ Pr[X=0] = 1-p$
換句話說、伯努力試驗是一種 YES or NO (1 or 0) 的試驗。舉例而言,像是「丟銅版、生男生女、 一地區某天最高溫是否超過 30 度」等等,都可以用伯努力實驗描述。
二項分布的意義
如果我們進行 n 次的伯努力試驗,而且這些試驗之間是獨立的,那麼我們就可以用二項分布來描述 n 次實驗的可能機率分布。
二項分布公式
分布公式:$f(x) = {n \choose x} p^x (1-p)^{n-x}$
意義:dbinom(x; n, p):在 n 次柏努力試驗中有 x 次成功的機率 (已知單次試驗成功機率為 p)。
R 的公式:dbinom(x; n, p) = p(x) = choose(n,x) p^x (1-p)^(n-x)
- R 函數:binom(size=n:樣本數, prob=p:成功機率)
- http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Binomial.html
二項定理: $(a+b)^n = \sum^{n}_{k=0} {n \choose k} a^k b^{n-k}$
特性
- $E(X) = \mu = np$
- $Var(X) = \sigma^2 = np (1-p) = npq$
動差生成函數: $m_x(t) = ((1-p)+pe^t)^n = (q+pe^t)^n$
習題
- 請問丟 10 個公平的銅板,有三個正面的機會是多少?
- 請問丟 n 個公平的銅板,正面次數 <= k 的機率是多少?
- 請問丟 10 個公平的銅板,得到正面次數的期望值為何?
R 程式範例:伯努力試驗
> y <- rbinom(50, 25, .4)
> m1 <- mean(y)
> m2 <- sum(y) / 25
> y
[1] 12 9 9 9 12 11 10 11 5 7 8 7 16 6 12 13 9 12 9 13 7 12 15 8
[25] 9 7 10 4 10 10 9 10 13 8 10 14 8 11 11 10 10 9 7 13 5 5 11 13
[49] 9 8
> m1
[1] 9.72
> m2
[1] 19.44
> m3 <- sum ( (y-m1)^2 ) / 50
> m3
[1] 6.8816
>
說明: y 中的每個數字,代表模擬投擲 25 次白努力試驗後,成功的次數有幾次。因此 rbinom(50, 25, .4) 總共進行了 50*25 次白努力試驗。
R 程式範例:二項分布曲線圖
> n=10; p=0.3; k=seq(0,n)
> plot(k, dbinom(k,n,p), type='h', main='dbinom(0:20, n=10, p=0.3)', xlab='k')
>

R 程式範例:(定理) 常態分配可用來逼近二項分布
假如 n 夠大的話,通常只要 n*min(p, 1-p) > 5 就可以採用下列逼近方式
$binom(n, p) \rightarrow norm(np, np(1-p))$
原始程式:
op=par(mfrow=c(2,2))
n=3; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=3, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=5; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=5, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=10; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=10, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
n=100; p=0.3; k=seq(0,n)
plot(k, dbinom(k,n,p), type='h', main='dbinom(n=100, p=0.3)', xlab='k')
curve(dnorm(x,n*p,sqrt(n*p*(1-p))), add=T, col='blue')
輸出圖形:

R 程式範例:二項分布統計圖
> x = rbinom(100000, 100, 0.8)
> hist(x, nclas=max(x)-min(x)+1)
>

參考文獻
- Distributions in the stats package – http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Distributions.html
- Wikipedia:二項分佈 – http://zh.wikipedia.org/wiki/%E4%BA%8C%E9%A0%85%E5%88%86%E4%BD%88
- Wikipedia:Binomial_distribution – http://en.wikipedia.org/wiki/Binomial_distribution
多項分布 (Multinomial Distribution)
$\frac{n!}{x_1!…x_k!} p_1^{x_1} p_2^{x_2}…p_k^{x_k}$
- 意義:n 次試驗中各種情況分別出現 x1, x2, …, xk 次的機率
- 範圍:x1, x2, …, xk=0,1,2,…,n ; 0<p[i]<1
- R 函數:multinom(size, prob) ; n:size:樣本數, p:prob:各種情況的機率
R 函數範例
rmultinom(10, size = 12, prob=c(0.1,0.2,0.8))
pr <- c(1,3,6,10) # normalization not necessary for generation
rmultinom(10, 20, prob = pr)
## all possible outcomes of Multinom(N = 3, K = 3)
X <- t(as.matrix(expand.grid(0:3, 0:3))); X <- X[, colSums(X) <= 3]
X <- rbind(X, 3:3 - colSums(X)); dimnames(X) <- list(letters[1:3], NULL)
X
round(apply(X, 2, function(x) dmultinom(x, prob = c(1,2,5))), 3)
執行結果:
> rmultinom(10, size = 12, prob=c(0.1,0.2,0.8))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 0 2 0 1 1 0 2
[2,] 1 2 3 0 3 0 2 1 1 2
[3,] 10 9 8 12 7 12 9 10 11 8
>
> pr <- c(1,3,6,10) # normalization not necessary for generation
> rmultinom(10, 20, prob = pr)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 2 2 1 1 2 1 1 2
[2,] 2 2 2 2 6 7 3 5 4 4
[3,] 9 4 8 4 8 8 4 7 3 6
[4,] 8 13 8 12 5 4 11 7 12 8
>
> ## all possible outcomes of Multinom(N = 3, K = 3)
> X <- t(as.matrix(expand.grid(0:3, 0:3))); X <- X[, colSums(X) <= 3]
> X <- rbind(X, 3:3 - colSums(X)); dimnames(X) <- list(letters[1:3], NULL)
> X
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
a 0 1 2 3 0 1 2 0 1 0
b 0 0 0 0 1 1 1 2 2 3
c 3 2 1 0 2 1 0 1 0 0
> round(apply(X, 2, function(x) dmultinom(x, prob = c(1,2,5))), 3)
[1] 0.244 0.146 0.029 0.002 0.293 0.117 0.012 0.117 0.023 0.016
>
負二項分布 (Netative binomial distribution)
公式:$f(x) = {x-1 \choose r-1} (1-p)^{x-r} p^r$
範圍:r=1,2,3,…. ; x= r, r+1, r+2, ….
意義:要得到第 r 次成功所需要的試驗次數 x;
R 函數: nbinom(size, prob) ; r:size:成功數, p:prob:成功機率
特性
- $E(X) = r/p$
- $Var(X) = r (1-p)/p^2 = r q/p^2$
動差生成函數:$m_x(t) = \frac{(pe^t)^r}{(1-(1-p) e^t)^r} = \frac{(p e^t)^r}{(1-q e^t)^r}$
習題
請問丟公平的銅板時,在得到第三次正面的要求下,其投擲次數 x 的機率分布為何?該分布的期望值為何?
請問丟公平的銅板時,在得到第 r 次正面的要求下,其投擲次數 x 的機率分布為何?該分布的期望值為何?
R 程式範例:負二項分布曲線圖
> n=20; p=0.4; k=seq(0,50)
> plot(k, dnbinom(k,n,p), type='h', main='dnbinom(k,n=20,p=0.4)', xlab='k')
>

> x = rnbinom(100000, 100, 0.8)
> hist(x, nclass=max(x)-min(x)+1)
>

R 程式範例 (進階)
require(graphics)
x <- 0:11
dnbinom(x, size = 1, prob = 1/2) * 2^(1 + x) # == 1
126 / dnbinom(0:8, size = 2, prob = 1/2) #- theoretically integer
## Cumulative ('p') = Sum of discrete prob.s ('d'); Relative error :
summary(1 - cumsum(dnbinom(x, size = 2, prob = 1/2)) /
pnbinom(x, size = 2, prob = 1/2))
x <- 0:15
size <- (1:20)/4
persp(x,size, dnb <- outer(x, size, function(x,s) dnbinom(x,s, prob= 0.4)),
xlab = "x", ylab = "s", zlab="density", theta = 150)
title(tit <- "negative binomial density(x,s, pr = 0.4) vs. x & s")
image (x,size, log10(dnb), main= paste("log [",tit,"]"))
contour(x,size, log10(dnb),add=TRUE)
## Alternative parametrization
x1 <- rnbinom(500, mu = 4, size = 1)
x2 <- rnbinom(500, mu = 4, size = 10)
x3 <- rnbinom(500, mu = 4, size = 100)
h1 <- hist(x1, breaks = 20, plot = FALSE)
h2 <- hist(x2, breaks = h1$breaks, plot = FALSE)
h3 <- hist(x3, breaks = h1$breaks, plot = FALSE)
barplot(rbind(h1$counts, h2$counts, h3$counts),
beside = TRUE, col = c("red","blue","cyan"),
names.arg = round(h1$breaks[-length(h1$breaks)]))
執行結果:
> require(graphics)
> x <- 0:11
> dnbinom(x, size = 1, prob = 1/2) * 2^(1 + x) # == 1
[1] 1 1 1 1 1 1 1 1 1 1 1 1
> 126 / dnbinom(0:8, size = 2, prob = 1/2) #- theoretically integer
[1] 504.0 504.0 672.0 1008.0 1612.8 2688.0 4608.0 8064.0 14336.0
>
> ## Cumulative ('p') = Sum of discrete prob.s ('d'); Relative error :
> summary(1 - cumsum(dnbinom(x, size = 2, prob = 1/2)) /
+ pnbinom(x, size = 2, prob = 1/2))
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.22e-16 -2.22e-16 -2.22e-16 -1.48e-16 0.00e+00 0.00e+00
>
> x <- 0:15
> size <- (1:20)/4
> persp(x,size, dnb <- outer(x, size, function(x,s) dnbinom(x,s, prob= 0.4)),
+ xlab = "x", ylab = "s", zlab="density", theta = 150)
> title(tit <- "negative binomial density(x,s, pr = 0.4) vs. x & s")
>
> image (x,size, log10(dnb), main= paste("log [",tit,"]"))
> contour(x,size, log10(dnb),add=TRUE)
>
> ## Alternative parametrization
> x1 <- rnbinom(500, mu = 4, size = 1)
> x2 <- rnbinom(500, mu = 4, size = 10)
> x3 <- rnbinom(500, mu = 4, size = 100)
> h1 <- hist(x1, breaks = 20, plot = FALSE)
> h2 <- hist(x2, breaks = h1$breaks, plot = FALSE)
> h3 <- hist(x3, breaks = h1$breaks, plot = FALSE)
> barplot(rbind(h1$counts, h2$counts, h3$counts),
+ beside = TRUE, col = c("red","blue","cyan"),
+ names.arg = round(h1$breaks[-length(h1$breaks)]))
繪圖結果:

參考文獻
幾何分布 (Geometric distribution)
$P(X=x) = (1-p)^{x-1} p = q^{x-1} p$
範圍:r=1,2,3,…. ; x= r, r+1, r+2, ….
意義:第一次成功所需要的試驗次數。
R 函數: geom(prob) ; p:prob:成功機率, x-1:size:失敗次數, q:失敗機率
- R 的公式:$p(x) = p (1-p)^x$
- R 當中的 x 代表失敗次數,而非第一次成功的次數,因此 R 當中的 x 相當於上式中的 (x-1)
- http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Geometric.html
特性:
- $E = 1/p$
- $Var(X) = \frac{(1-p)}{p^2} = \frac{q}{p^2}$
動差生成函數:$m_x(t) = \frac{p e^t}{1-(1-p) e^t}= \frac{p e^t}{1-q e^t}$
R 程式範例:曲線圖
p=0.7; k=seq(0,10)
plot(k, dgeom(k, p), type='h', main='dgeom(p=0.5)', xlab='k')
R 程式範例:
qgeom((1:9)/10, prob = .2)
Ni <- rgeom(20, prob = 1/4); table(factor(Ni, 0:max(Ni)))
執行結果:
> qgeom((1:9)/10, prob = .2)
[1] 0 0 1 2 3 4 5 7 10
> Ni <- rgeom(20, prob = 1/4); table(factor(Ni, 0:max(Ni)))
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
4 5 3 2 0 3 1 0 0 0 1 0 0 0 0 0 0 1
>
參考
布瓦松分布 (Poisson distribution)
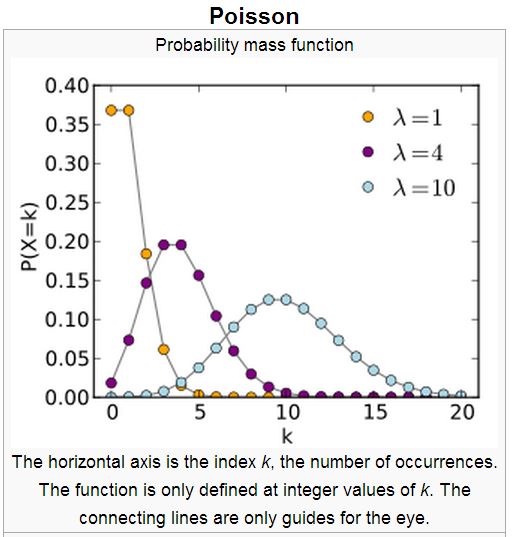
意義:在單位時間內,事件出現平均 λ 次的機率分布。
公式:$f(x) = \frac{e^{-k} k^x}{x!}$
R 的公式: $p(x) = \lambda^x e^{-\lambda}/x!$
R 函數:pois(λ:事件平均出現次數)
變數意義:$k = \lambda$
特性:
布瓦松分布可以與泰勒展開式中的 Maclaurin 級數對映起來,所謂的 Maclaurin 級數就是泰勒展開式在 0 點的展開式。
If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
$e^x = 1+x+x^2/2!+x^3/3!+ … + x^k/k! + ….$
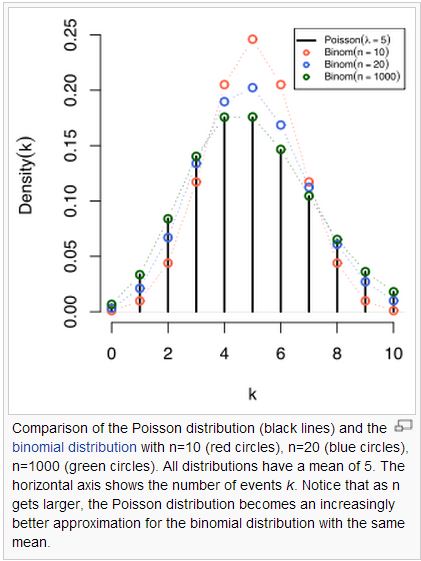
布瓦松分配的公式來源
布瓦松分配可視為二項分配的極限形式,當 binom(n, p) 當中 n 趨近於無限大,而 p 非常小的時候,就會趨近布瓦松分配。
關鍵公式:$\lim_{n\to\infty}\left(1-{\lambda \over n}\right)^n=e^{-\lambda}$
證明過程:
$\lim_{n\to\infty} P(X_n=k) = \lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k}=\lim_{n\to\infty} {n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}$ .
$=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}{A_n}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}$ .
$=\left[ \lim_{n\to\infty} A_n \right] \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\to\left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)$ .
其中的 An 趨近於 1 ,證明如下:
$A_n= \frac{n!}{n^k\left(n-k\right)!}= \frac{n\cdot (n-1)\cdots \big(n-(k-1)\big)}{n^k}=1\cdot(1-\frac{1}{n})\cdots(1-\frac{k-1}{n})\to 1\cdot 1\cdots 1 = 1$ .
期望值與變異數
- $E(X) = k = \lambda$
- $Var(X) = k = \lambda$
動差生成函數:$m_x(t) = e^{k (e^t-1) } = e^{\lambda (e^t-1) }$
習題:
習題:抽血時白血球數量的問題
問題: 假如現在從你身上抽一滴血,請回答下列兩個問題。
- 請定義一個隨機變數 X 代表那滴血中的白血球數量。
提示: 樣本空間 S = 此時此刻你身上的所有白血球 = {w1,w2,……,wn}
- 請算出一滴血液中有三顆白血球的機率,假設該滴血液占你總血量的 1/1000。
解答 1:
X(A) = |A|
說明:
A 是一個事件,也就是白血球的樣本空間 S 的子集合,例如: A = {w1, w5, w9}
|A| 代表 A 集合的大小,也就是元素個數,舉例而言:
如果 A = {w1, w5, w9} ,那麼 |A| = 3
如果 B = {w2, w8},那麼 |B| = 2
如果 C = {},那麼 |C| = 0
如果 D = S,那麼 |D| = n
解答 2:
P(X=3) = P({A | X(A) = 3}) = P({w1, w2, w3}) + P({w1, w2, w4}) + ……
假如任一顆白血球被抽到的機率等於該滴血液佔全身血液的比率,由於該滴血液佔總血量的 1/1000,所以給顆白血球被抽到的機率為 1/1000。
而且假設這些白血球沒有智慧,也不會聚合在一起,因此相互之間獨立,那麼由於每顆白血球被抽到的機率為 1/1000,因此 P(w1) = P(w2) = …. P(wn) = 1/1000。
那麼初步想法是 P(w1w3) = P(w1) * P(w3) = 1/1000 * 1/1000 。
但是上述的想法有個小問題,那就是該情況代表其它白血球都沒被抽到,因此所謂的 P(w1w3) 真正的意思應該是
$P(w_1 \bar{w_2} w_3 \bar{w_4} …. \bar{w_n}) = (\frac{1}{1000})^2 (\frac{999}{1000})^{n-2}$
所以 P(X=3) 應該算法如下:
$P(X=3) = P({A| X(A) = 3}) = (\frac{1}{1000})^3 (\frac{999}{1000})^{n-3} {n \choose 3}$
推而廣之,P(X=k) 的機率之算法如下:
$P(X=k) = P({A| X(A) = k}) = (\frac{1}{1000})^k (\frac{999}{1000})^{n-k} {n \choose k}$
事實上,這個題目的機率分布就是下一章的二項分布,如下所示:
$P(X=k) = {n \choose k} p^k (1-p)^{n-k}$
而且、當 n 趨近於無限大時,這個分布將會趨近於布瓦松分布,如下所示:
$P(X=k) = \lambda^k e^{-\lambda}/k!$
其中的 λ 之意義為,在單位時間 (或單位面積、體積) 內,事件的出現次數平均為 λ 次。
習題:假設每 1CC 的血所含的白血球平均為 10 顆,那麼請問你抽 1CC 的血時,抽到 8 顆白血球的機率是多少。
解答:
λ = 10,因此布瓦松分布為 $p(x) = 10^x e^{-10}/x!$ ,將 x=8 代入,得到 $p(8) = 10^8 e^{-10}/8!$
其數值可以用 R 軟體計算,如下所示:
> ?dpois
> dpois(8, 10)
[1] 0.112599
> 10^8*exp(-10)/prod(1:8)
[1] 0.112599
R 程式範例:曲線圖
lambda=5.0; k=seq(0,20);
plot(k, dpois(k, lambda), type='h', main='dpois(lambda=4.0)', xlab='k')

R 程式範例:
require(graphics)
-log(dpois(0:7, lambda=1) * gamma(1+ 0:7)) # == 1
Ni <- rpois(50, lambda = 4); table(factor(Ni, 0:max(Ni)))
1 - ppois(10*(15:25), lambda=100) # becomes 0 (cancellation)
ppois(10*(15:25), lambda=100, lower.tail=FALSE) # no cancellation
par(mfrow = c(2, 1))
x <- seq(-0.01, 5, 0.01)
plot(x, ppois(x, 1), type="s", ylab="F(x)", main="Poisson(1) CDF")
plot(x, pbinom(x, 100, 0.01),type="s", ylab="F(x)",
main="Binomial(100, 0.01) CDF")
執行結果:
> require(graphics)
>
> -log(dpois(0:7, lambda=1) * gamma(1+ 0:7)) # == 1
[1] 1 1 1 1 1 1 1 1
> Ni <- rpois(50, lambda = 4); table(factor(Ni, 0:max(Ni)))
0 1 2 3 4 5 6 7 8
1 3 6 8 11 11 4 3 3
>
> 1 - ppois(10*(15:25), lambda=100) # becomes 0 (cancellation)
[1] 1.233094e-06 1.261664e-08 7.085799e-11 2.252643e-13 4.440892e-16
[6] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[11] 0.000000e+00
> ppois(10*(15:25), lambda=100, lower.tail=FALSE) # no cancellation
[1] 1.233094e-06 1.261664e-08 7.085800e-11 2.253110e-13 4.174239e-16
[6] 4.626179e-19 3.142097e-22 1.337219e-25 3.639328e-29 6.453883e-33
[11] 7.587807e-37
>
> par(mfrow = c(2, 1))
> x <- seq(-0.01, 5, 0.01)
> plot(x, ppois(x, 1), type="s", ylab="F(x)", main="Poisson(1) CDF")
> plot(x, pbinom(x, 100, 0.01),type="s", ylab="F(x)",
+ main="Binomial(100, 0.01) CDF")
>
