抽樣與敘述統計
隨機抽樣
統計的基礎是抽樣,所謂的抽樣就是從母體 (一大群樣本) 當中抽出一些樣本,而在抽樣的時候,我們通常會盡可能的確保樣本的隨機性,以避免抽到的樣本有所偏差。
簡單來說,抽樣是從一群東西(母體) 當中隨機抽取出 x1, x2, …., xn 等 n 個觀察值的過程,表示如下:
母體 => (獨立性) X1, X2, .... , Xn 等 n 個隨機變數相互獨立 =>
取出 x1, x2, ...., xn 等 n 個觀察值。
在電腦上,我們可以很容易的模擬隨機抽樣,以下是一個使用 R 軟體模擬隨機抽樣的範例,其中指令 sample(1:100, 10) 代表從 1 到 100 的整數當中取出 10 個樣本出來。
> x = sample(1:100, 10)
> x
[1] 12 17 50 33 98 77 39 79 7 26
sample 函數的原型是 sample(x, size, replace = FALSE, prob = NULL),如果 replace 設定為 FALSE,代表已經取過就會被去除,不能重複出現;反之則可以重複出現。
在統計學中,有一些常用的機率模型,都有對應的 R 函數,以下是一些最常用的機率模型之整理。
| 機率模型 | 密度函數 | R 函數名稱 | 說明 |
|---|---|---|---|
| 二項分布 | ${n \choose x} p^x (1-p)^{n-x}$ | binom(n:size, p:prob) | n:樣本數, p:正面機率, n 次試驗中有 x 個成功的機率 |
| 布瓦松分布 | $\frac{e^{-\lambda} {\lambda}^x}{x!}$ | pois(lambda) | 在每單位區域內,事件出現平均 $\lambda$ 次 |
| 均勻分布 (Uniform) | $\frac{1}{b-a}$ | unif(a:min, b:max) | a:範圍下限, b: 上限 出現機會均等 |
| 常態分布(Normal) | $\frac{1}{\sqrt{2\pi} \sigma} e^{- \frac{1}{2} [(x-\mu)/\sigma]^2}$ | norm(mean, sd) | 中央極限定理:x1+x2+…+xk; 當 k 越大就越接近常態分布 |
| 指數分布 (Exponential) | $\frac{1}{b} e^{-x/b}$ | exp(rate) | 伽瑪分布($a=1, b=\frac{1}{\lambda}$) 布瓦松過程中,第一次事件出現的時間 W |
對於每個機率模型,您只要在該函數前若加入 r 這個字,就可以用來產生隨機樣本,以下是一些隨機樣本的產生範例。
> rbinom(20, 5, 0.5)
[1] 4 3 3 4 2 4 3 1 2 3 4 3 2 2 2 4 2 3 1 1
> rpois(20, 3.5)
[1] 2 1 4 2 1 6 3 6 1 3 3 6 6 0 4 2 6 4 6 2
> runif(20, min = 3, max = 8)
[1] 3.933526 3.201883 7.592147 5.207603 4.897806 3.848298 4.521461 4.437873
[9] 3.655640 5.633540 6.557995 5.430671 6.502675 5.637283 7.713699 5.841052
[17] 6.859493 5.987991 3.752924 7.480678
> rnorm(20, mean = 5.0, sd = 2.0)
[1] 6.150209 4.743013 3.328734 5.096294 4.922795 6.272768 4.862825 8.036376
[9] 4.198432 5.467984 2.046450 6.452511 2.088256 5.349187 3.074408 3.628072
[17] 3.421388 7.242598 3.125895 9.865341
> rexp(20, rate=2.0)
[1] 0.17667426 0.49729383 0.12786107 0.13983412 0.44683515 1.30482842
[7] 0.28512544 1.61472266 0.23220649 0.39089780 0.05947224 1.42892610
[13] 0.02555552 0.69409186 0.68228242 0.22542362 0.33590791 0.14684937
[19] 0.34995146 0.80595369
為了讓讀者能確認這些指令所產生的圖形確實符合分布,讓我們用這些隨機抽樣函數各產生 100,000 個樣本, 然後用 hist() 這個函數繪製統計圖,就能看出這些抽樣函數的效果了,以下是我們的抽樣指令與結果圖形。
> x = rbinom(100000, 5, 0.5)
> hist(x)
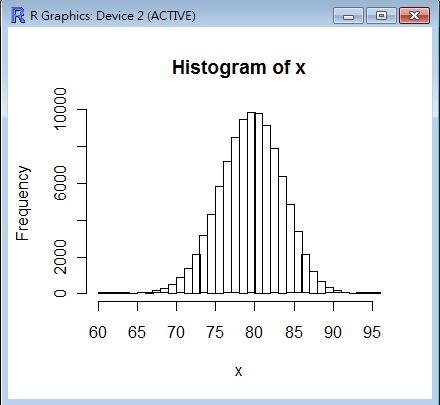
> y = rpois(100000, 3.5)
> hist(y)
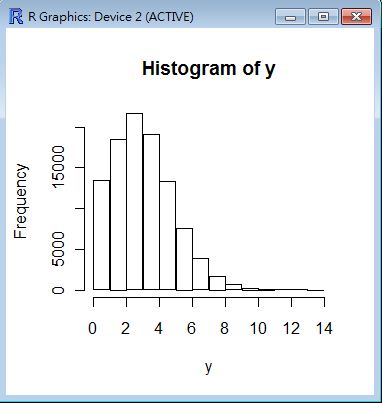
> z = runif(100000, min=3, max=8)
> hist(z)
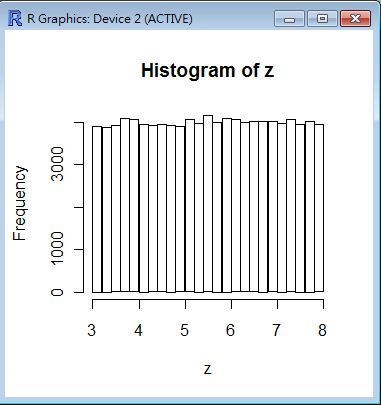
> w = rnorm(100000, mean=5.0, sd=2.0)
> hist(w)

> v = rexp(100000, rate=2.0)
> hist(v)
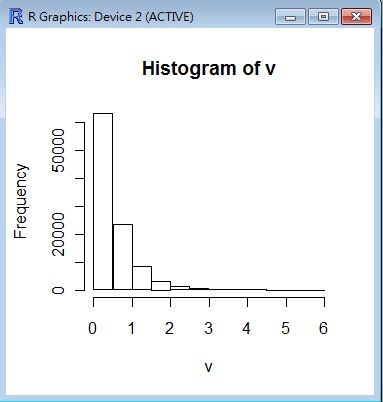
單組樣本的敘述統計
敘述統計乃是隨機抽樣的樣本集合,進行某些計算與繪圖,以便忠實的呈現出樣本的某些特性。這些計算出的數值,以及呈現出來的圖形,可以反映出樣本的某些統計特性,讓統計者能透過數值或圖形,大致了解樣本的統計特徵。
| 中文名稱 | 英文名稱 | 數學公式 / 說明 |
|---|---|---|
| 樣本平均數 | Mean | $\bar{X} = \frac{\sum_{i=1}^n X_i}{n}$ |
| 樣本中位數 | Median | 樣本排序後最中間位置的數值 |
| 樣本變異數 | Sample Variance | $S^2 = \sum_{i=1}^n \frac{(X_i - \bar{X})^2}{n-1} = \frac{n \sum_{i=1}^n X_i^2 - (\sum_{i=1}^n Xi)^2}{n (n-1)}$ |
| 樣本標準差 | Sample Standard Deviation | 樣本變異數中的 S 稱為樣本標準差,也就是 $\sqrt{S^2}$ |
| 樣本全距 | Range | 樣本中最大的觀察值減去最小的觀察值 $\omega = X_H-X_L$ |
| 離群值 | Outlier 或 Wild | 離其他樣本很遠,特別大或特別小的樣本值 |
| 樣本四分數間距 | InterQuartile Range, IQR | 第 3 四分位數減掉第 1 四分位數 $IQR = q_3 - q_1$ |
注意:變異數的定義為 $\delta^2 = E[(X-\mu)^2]$,上述的樣本變異數必須除以 n-1 才是變異數的不偏估計量,而不是除以 n (這是因為我們並不知道母體真正的 $\mu$ 值是多少,因此採用了 $X-\bar{X}$ 來代替 $X-\mu$ ,但是這樣就會造成多減掉 一份樣本的效應,於是分母就必須除以 n-1 了)。
範例:請寫出樣本序列 (7 4 6 8 9 4 5 6 2 8) 的以下敘述統計值與其計算過程。
- 樣本平均數 (Mean)
- 樣本變異數 (Sample Variance)
- 樣本標準差 (Sample Standard Deviation)
- 中位數 (Median)
- 全距 (Range)
- 第一四分位數 (q1)
- 第三四分位數 (q3)
- 樣本四分數間距 (iqr)
解答:
- 樣本平均數 (Mean)
mean(x) = (7+4+6+8+9+4+5+6+2+8)/10 = 5.9
- 樣本變異數 (Sample Variance)
$var(x) = \frac{(7-5.9)^2+(4-5.9)^2+(6-5.9)^2+(8-5.9)^2+(9-5.9)^2+(4-5.9)^2+(5-5.9)^2+(6-5.9)^2+(2-5.9)^2+(8-5.9)^2}{10-1} = 4.77$
- 樣本標準差 (Sample Standard Deviation)
$S = sqrt(var(x)) = sqrt(4.77)$
- 中位數 (Median)
M = (2 4 4 5 6 6 7 8 8 9) 最中間的值 = (6+6)/2 = 6
- 全距 (Range)
range(x) = 9-2 = 7
- 第一四分位數 (q1)
順序 0 1 2 3 4 5 6 7 8 9
樣本 2 4 4 5 6 6 7 8 8 9
q1 的位置 0.25 * 9/10 = 0.225
所以 q1 = 4+0.25 * (5-4) = 4.25
- 第三四分位數 (q3)
q3 的位置 0.75 * 9/10 = 0.675
所以 q3 = 7+0.75 * (8-7) = 7.75
- 樣本四分數間距 (iqr)
iqr(x) = q3-q1 = 7.75-4.25 = 3.5
使用 R 軟體進行驗證
> x = sample(1:100, 10)
> x
[1] 12 17 50 33 98 77 39 79 7 26
> mean(x)
[1] 43.8
> median(x)
[1] 36
> var(x)
[1] 984.1778
> sd(x)
[1] 31.37161
> range(x)
[1] 7 98
> max(x)
[1] 98
> min(x)
[1] 7
> max(x)-min(x)
[1] 91
> q1 = quantile(x, 0.25)
> q1
25%
19.25
> q3 = quantile(x, 0.75)
> q3
75%
70.25
> q3-q1
75%
51
> iqr(x)
錯誤: 沒有這個函數 "iqr"
> IQR(x)
[1] 51
> fivenum(x)
[1] 7 17 36 77 98
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
7.00 19.25 36.00 43.80 70.25 98.00
習題:請用 R 軟體計算出樣本序列 (8.9 , 4.5 , 3.7 , 10.0 , 11.5 , 8.9 , 5.6 , 15.4 , 16.6 , 1.0) 的以下敘述統計值 (必須寫出指令與結果)。
樣本平均數 (Mean)
樣本變異數 (Sample Variance)
樣本標準差 (Sample Standard Deviation)
中位數 (Median)
全距 (Range)
第一四分位數 (q1)
第三四分位數 (q3)
樣本四分數間距 (iqr)
解答:
[1] 25.37433
> sd(x)
[1] 5.037294
> median(x)
[1] 8.9
> max(x)-min(x)
[1] 15.6
> q1 = quantile(0.25, x)
錯誤在quantile.default(0.25, x) : 'probs' outside [0,1]
> q1 = quantile(x, 0.25)
> q1
25%
4.775
> q3 = quantile(x, 0.75)
> q3
75%
11.125
> q3-q1
75%
6.35
> IQR(x)
[1] 6.35
>
繪製統計圖
| 中文名稱 | 英文名稱 | R 指令 | 說明 |
|---|---|---|---|
| 直方圖 | Histogram | hist(x) | 根據每個區間的樣本出現次數繪製的長條圖。 |
| 莖葉圖 | Stem-and-Leaf Diagram | stem(x) | 用主幹數字與分支數字表示分布情況的圖形。 |
| 盒型圖 | Boxplots | boxplot(x) | 由平均值、內籬笆與外籬笆所形成的盒型圖,可看出中心點與離散程度。 |
| 肩型圖 (累加分配圖) | Relative Cumulative Frequency Ogive | plot(ecdf(x)) | 將累加次數繪製出來的圖形。 |
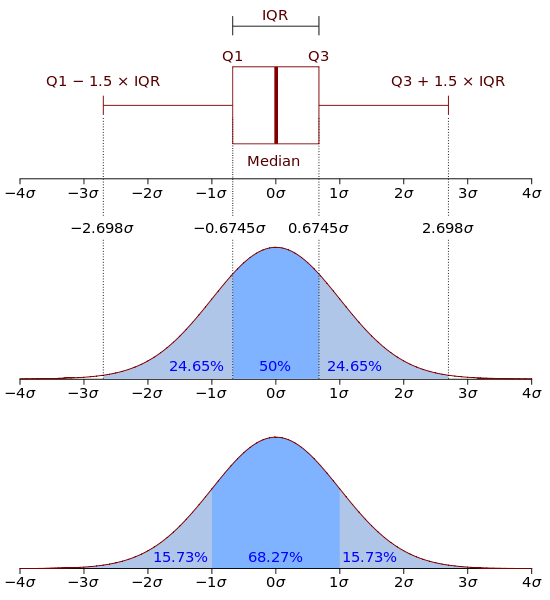
說明:盒型圖是由四分位數 q1, q3, 以及內籬笆 f1, f3 (inner fences), 連接值 a1, a3 與外籬笆 F1, F3 (outer fances) 所組成的圖形
- 內籬笆:f1 = q1 - 1.5 iqr; f3 = q3 + 1.5 iqr;
- 外籬笆:F1 = q1 - 3.0 iqr; F3 = q3 + 3.0 iqr;
- 連接值:a1 是大於且最接近 f1 的數據點; a3 小於且最接近 f3 的數據點。
盒型圖的畫法請參考下列圖形:
R 操作範例 : 統計圖
> x = rnorm(100)
> x
[1] 0.389381081 -0.274522826 1.492670583 -1.563228609 0.766405108
[6] 0.736573742 0.297407135 -1.324130406 -1.376598231 1.661727175
[11] -1.356590351 1.309122339 -1.193821085 0.365801091 -0.952034088
[16] -0.277610568 -0.599980091 -0.124105876 -1.107713162 0.560637570
[21] 0.714449138 0.111969057 0.505171739 -2.418297599 0.318797182
[26] 2.716646516 0.345289422 0.019434615 1.087758951 0.033917165
[31] -0.356786424 -1.284809066 1.580411327 0.552931291 -0.615928762
[36] -0.087069820 -0.814632197 -0.570882510 -0.107731447 -1.453838416
[41] -0.257115209 1.166866120 1.072692716 -0.022594852 0.441221144
[46] 1.053900960 -1.025193547 -1.119200587 0.264668203 1.409504515
[51] 0.241644132 -0.955407800 0.446297381 0.231887649 0.769308731
[56] 0.269624579 0.496109294 0.822638573 -0.904380789 -0.429527404
[61] -2.050582772 -0.586973281 -1.192753403 1.158321933 -0.151319360
[66] 0.558858868 -0.656174351 -2.858964403 0.366785049 0.896958092
[71] 0.369315063 -0.953560954 -0.762608370 -1.017449547 -0.127738562
[76] -1.922030980 -0.839897930 1.332972530 -0.001151104 0.104336360
[81] -0.208907813 1.401335798 0.019330593 -0.687559289 0.445371885
[86] 0.504532689 2.168626000 -1.742886230 0.831058071 2.011604088
[91] 1.676059594 1.132849957 -1.047073217 -0.912548540 -2.235854777
[96] -1.194104128 0.121106118 -1.178415224 0.214196778 0.280714044
> stem(x)
The decimal point is at the |
-2 | 9421
-1 | 97654433222211000000
-0 | 998887766664433322111100
0 | 00011122233333344444445556667788889
1 | 11112233445677
2 | 027
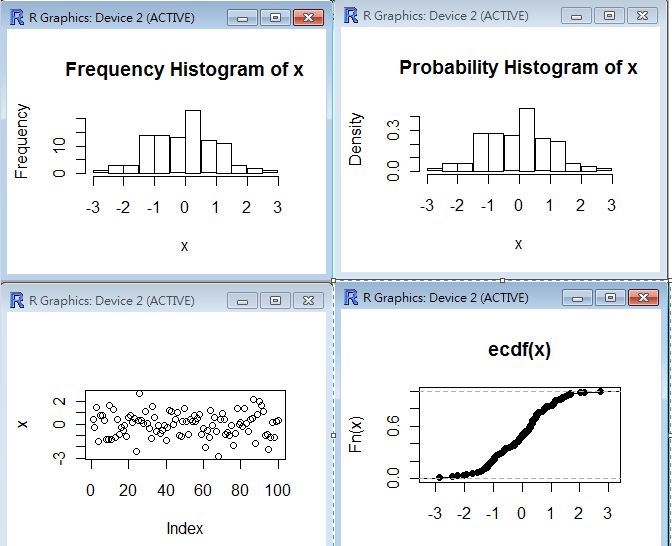
> hist(x, main="Frequency Histogram of x")
> hist(x, main="Probability Histogram of x", freq=F)
> Fx = ecdf(x)
> plot(x)
> plot(Fx)
> boxplot(x)
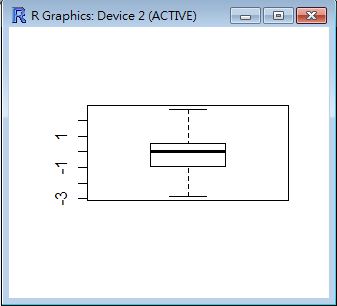
以上都是對於單組樣本的統計數字與圖形,以下將討論兩組樣本的統計數字
共變異數、兩組樣本的相關度統計
兩組樣本的統計數字,最重要的就是共變異數 (covariance) 相關係數 (correlation) 與了。
共變異數是兩組樣本 X, Y 的樣本與期望值之間差的乘積之期望值,而相關係數則共變異數經過 正規化後的結果,用來表示兩組樣本相關程度,其數值介於 -1.0 到 1.0 之間。
中文名稱 英文名稱 R 指令 數學公式 / 說明
共變異數 covariance cov(x,y) $\gamma_{XY} =E[ (X-E[X]),(Y-E[Y])]$ 相關係數 correlation cor(x,y) $\phi_{XY} =E[ (X-E[X])(Y-E[Y])]/(\sigma_X \sigma_Y)$
讓我們看看 R 軟體中的共變異數函數 cov() 與相關係數 cor() 的操作,如下所示:
runif(10, 1, 5)
> x
[1] 1.375135 1.863417 2.403693 2.639902 1.694610 4.419406 4.032262 2.147783
[9] 1.501733 1.497732
> cov(x, x)
[1] 1.144697
> cov(x, x+1)
[1] 1.144697
> cor(x, x)
[1] 1
> cor(x, x+1)
[1] 1
> cov(x, -x)
[1] -1.144697
> cor(x, -x)
[1] -1
> cor(x, 0.5*x)
[1] 1
> y = runif(10, 1, 5)
> y
[1] 1.114662 2.358270 2.089179 4.581484 4.170922 2.630044 1.450336 1.320637
[9] 1.705649 3.506064
> cor(x, y)
[1] -0.04560485
> cor(y, y)
[1] 1
>