中央極限定理
中央極限定理是機率統計上最重要的定理之一,整個統計的估計與檢定幾乎都建立在這個定理之上,因此 對「中央極限定理」有清楚的理解是學好機率統計的一個關鍵。
在本章中,我們將利用 R 軟體實作並驗證「中央極限定理」,讓讀者能透過程式實際體會該定理的重要性與用途。
但是在說明中央極限定理之前,先讓我們來看看一個更簡單的數學定律,那就是大數法則。
大數法則
大數法則又稱大數律,是個數學與統計學的概念,意指數量越多,則其平均就越趨近母體平均數 $\mu$。
用數學的講法來說,也就是如下的公式成立。
$ \bar{x}_n=\frac{x_1+x_2+…+x_n}{n} \to \mu$ ; 當 $n \to \infty$ 之時。
但是、在上述的趨近定義上,大數法則通常還可以分為強弱兩個版本,如下所示:
弱大數法則 (Weak law) : $\lim_{n \to \infty} P( |\bar{x}_n - \mu| > \epsilon ) = 0$
弱大數法則的意義是說,當樣本數趨近於無限大時,樣本平均值會趨近於母體平均數 $\mu$。
強大數法則 (Strong law) : $P( \lim_{n \to \infty} |\bar{x}_n = \mu| ) = 1$
而強大數法則的意義則是說,當樣本數趨近於無限大時,樣本平均值等於母體平均數 $\mu$ 的機率為 1。
上述的大數法則只是說出一個傾向而已,而且 $n \to \infty$ 這個要求太過強烈,現實上是不可能達到的, 如果能夠找到有限樣本下的平均數之變動範圍限制,那會比這樣的無限大要求更好一些。
柴比雪夫不等式
柴比雪夫不等式給出了樣本分佈情況的一個限制條件,其數學公式如下所示:
$P(\mu - k \sigma < X < \mu + k \sigma) \ge 1- \frac{1}{k^2}$
柴比雪夫不等式所述說的,是樣本平均數與標準差之間的一個限制關係,這個關係不管在哪一種分佈之下,都一定會成立的。
與平均數 $\mu$ 相差至少 2 個標準差 ( $2\sigma$ ) 的樣本數目不多於 1/4。
與平均數 $\mu$ 相差至少 3 個標準差 ( $3\sigma$ ) 的樣本數目不多於 1/9。
與平均數 $\mu$ 相差至少 4 個標準差 ( $4\sigma$ ) 的樣本數目不多於 1/16。
與平均數 $\mu$ 相差至少 k 個標準差 ( $k\sigma$ ) 的樣本數目不多於 $1/k^2$。
舉例而言,假如一個 40 人的班上,同學的平均體重為 50 公斤,標準差為 10 公斤,那麼體重小於 30 公斤的人不可能會超過 10 人。
初步看起來,柴比雪夫不等式非常得奇怪,感覺很不合理,舉例而言,對於 n 個柏努力試驗的樣本,由於樣本值不是 0 就是 1,這樣 應該會不符合柴比雪夫不等式才對,但事實上卻會符合。
讓我們舉一個例子,假如 20 個伯努力試驗,共有十次成功,十次失敗,於是其平均值、變異數與標準差可計算如下:
- 平均值: $\mu = \bar{X} = \frac{010 + 110}{20} = 0.5$
- 變異數: $\sigma^2 = E[(X-\mu)^2] = \frac{(0-0.5)^210 + (1-0.5)^210}{20} = \frac{0.25 * 20}{20} = 0.25$
- 標準差: $\sigma = \sqrt{0.25} = 0.5$
因此,與平均數 $\mu=0.5$ 相差兩個標準差的以上情況根本就不存在 (也就是 $P(\mu - 2 \sigma < X < \mu + 2 \sigma)=P(0.5 - 2 \times 0.5 < X < 0.5 + 2 \times 0.5)=P(-0.5 < X < 1.5)=1$ ,於是落在區域外的機率根本就是 0 ), 所以柴比雪夫不等式在這樣分為兩個極端的分布上還是會成立的。
雖然柴比雪夫不等式給出了平均值的範圍限制,但是卻沒有給出平均值分佈的形狀,還好中央極限定理解決了這個問題。
中央極限定理簡介
以下是中央極限定理的數學式:
$\frac{x_1+x_2+…+x_n}{n} = \bar{x} \rightarrow N(\mu, \sigma/\sqrt{n})$
如果用白話文陳述,那就是說 n 個樣本的平均數 $\frac{x_1+x_2+…+x_n}{n}=\bar{x}$ 會趨近於常態分布。
更精確一點的說,當您從某個母體 X 取出 n 個樣本,則這 n 個樣本的平均數 $\frac{x_1+x_2+…+x_n}{n}=\bar{x}$ 會趨近於以平均期望值 $\mu$ 為中心, 以母體標準差 $\sigma$ 除以 $\sqrt{n}$ 的值 $\sigma/\sqrt{n}$ 為標準差的常態分布。
如果採用另一種正規化後的公式寫法,也可以將上述的「中央極限定理」改寫為: $\frac{\bar{x}-\mu}{\sigma/\sqrt{n}} \rightarrow Z$
其中的 Z 是指標準常態分部,也就是 $\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}$ 會趨近標準常態分布。
中央極限定理的用途
根據上述的定義,我們知道當樣本數 n 足夠大時 (通常 20 個以上就夠大了), n 個樣本的平均值 $\frac{x_1+x_2+…+x_n}{n}=\bar{x}$ 會趨近於常態分布,換句話說也就是 $\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}$ 會趨近於標準常態分布。
因此、當我們取得一組樣本之後,我們就可以計算其平均數 $\frac{x_1+x_2+…+x_n}{n}=\bar{x}$,如果有人告訴我們說母體的 平均數 $\mu$ 的值是多少,我們就可以看看 $\bar{x}$ 與 $\mu$ 是否差距很遠,如果差距很遠, 導致 $\bar{x}$ 來自平均數 $\mu$ 母體的機率很小,那麼很可能是此組樣本是非常罕見的特例,或者該組樣本的抽樣有所偏差,也就是該組樣本很可能並非來自平均數為 $\mu$ 的母體。
以下是一些標準常態分布的重要數值,
- $P[-\sigma < X - \mu < \sigma] = 0.68$
- $P[-2 \sigma < X - \mu < 2 \sigma] = 0.95$
- $P[-3 \sigma < X - \mu < 3 \sigma] = 0.997$
- $P[-4 \sigma < X - \mu < 4 \sigma] = 0.99993$
- $P[-5 \sigma < X - \mu < 5 \sigma] = 0.9999994$
- $P[-6 \sigma < X - \mu < 6 \sigma] = 0.999999998$
> pnorm(1)-pnorm(-1)
[1] 0.6826895
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> pnorm(3)-pnorm(-3)
[1] 0.9973002
> pnorm(4)-pnorm(-4)
[1] 0.9999367
> pnorm(5)-pnorm(-5)
[1] 0.9999994
> pnorm(6)-pnorm(-6)
[1] 1
> options(digits=10)
> pnorm(6)-pnorm(-6)
[1] 0.999999998
從上面的數值您可以看出來,管理學上所謂的六標準差其實是很高的一個要求,也就是良率必須要達到 99.9999998% 以上才行。
如果您今天所取的 n 個樣本,與母體平均數 $\mu$ 距離兩個標準差以上,那就很可能有問題了,這種推論稱為檢定,我們可以用 R 軟體中的 t.test 函數來檢驗這件事,我們將在下一期當中說明如何用 R 軟體進行統計檢定的主題,讓我們先將焦點移回到中央極限定理身上,用 R 軟體 來驗證該定理。
R 程式範例:驗證中央極限定理
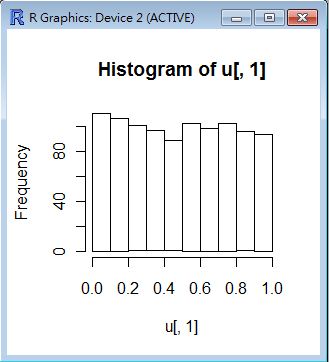
> u <- matrix ( runif(500000), 50, 10000 )
> y <- apply ( u, 2, mean )
> hist(u[,1])
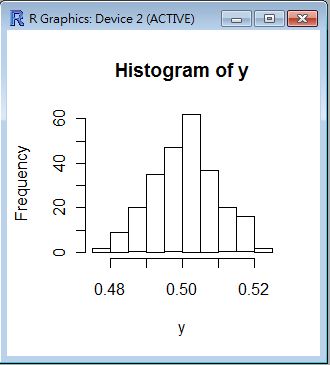
> hist(y)
> ?apply
>
說明:
- u 乃是將 50 萬個 uniform 樣本分配成 50*10000 的矩陣,
- y 對 u 進行列統計 apply ( u, 2, mean ) 代表對每行取平均值 mean(col of u) 的結果。
- 因此 y 代表從 Uniform Distribution 中每次取出 50 個樣本,然後進行加總平均的結果,也就是 $\frac{x_1+x_2+…+x_{50}}{50}$ 。
- 從下列的 hist(y) 圖形中,我們可以看到中央極限定理的證據:也就是 $\frac{x_1+x_2+…+x_{50}}{50}$ 會趨向常態分布。
CLT = function(x) {
op<-par(mfrow=c(2,2)) # 設為 2*2 的四格繪圖版
hist(x, nclass=50) # 繪製 x 序列的直方圖 (histogram)。
m2 <- matrix(x, nrow=2, ) # 將 x 序列分為 2*k 兩個一組的矩陣 m2。
xbar2 <- apply(m2, 2, mean) # 取每兩個一組的平均值 (x1+x2)/2 放入 xbar2 中。
hist(xbar2, nclass=50) # 繪製 xbar2 序列的直方圖 (histogram)。
m10 <- matrix(x, nrow=10, ) # 將 x 序列分為 10*k 兩個一組的矩陣 m10。
xbar10 <- apply(m10, 2, mean) # 取每10個一組的平均值 (x1+..+x10)/10 放入 xbar10 中。
hist(xbar10, nclass=50) # 繪製 xbar10 序列的直方圖 (histogram)。
m20 <- matrix(x, nrow=20, ) # 將 x 序列分為 25*k 兩個一組的矩陣 m25。
xbar20 <- apply(m20, 2, mean) # 取每20個一組的平均值 (x1+..+x20)/20 放入 xbar20 中。
hist(xbar20, nclass=50) # 繪製 xbar20 序列的直方圖 (histogram)。
}
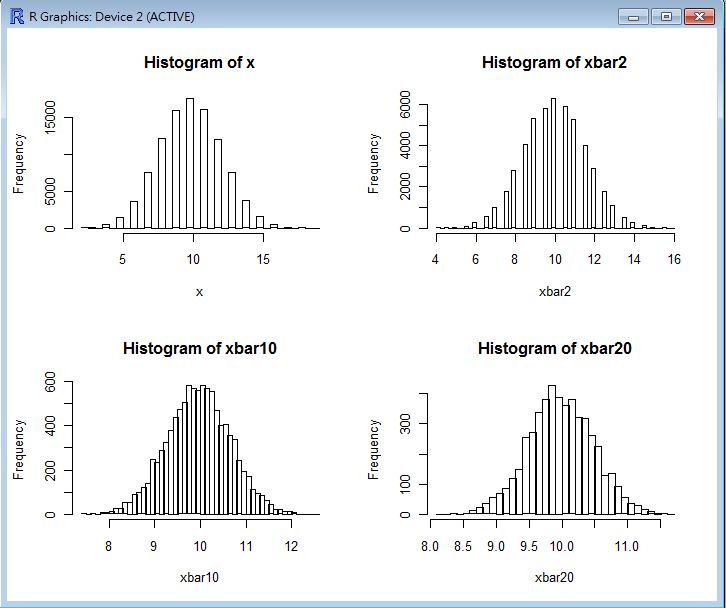
CLT(rbinom(100000, 20, 0.5)) # 用參數為 n=20, p=0.5 的二項分布驗證中央極限定理。
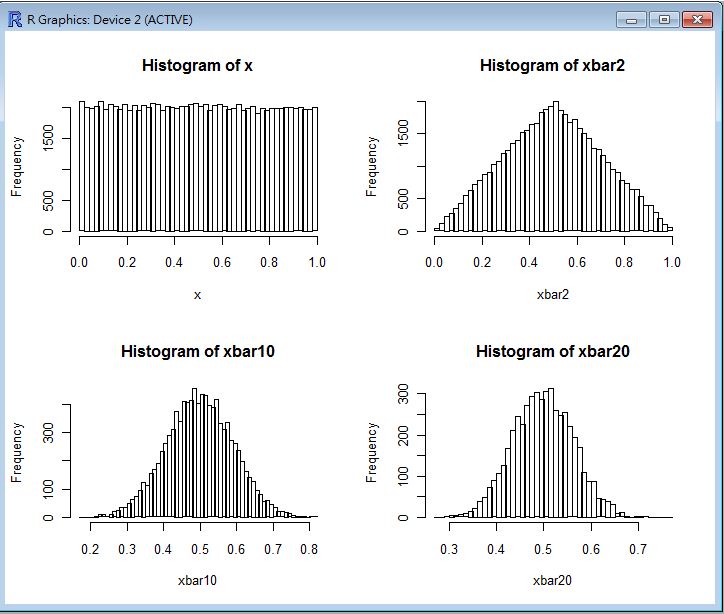
CLT(runif(100000)) # 用參數為 a=0, b=1 的均等分布驗證中央極限定理。
CLT(rpois(100000, 4)) # 用參數為 lambda=4 的布瓦松分布驗證中央極限定理。
CLT(rgeom(100000, 0.5)) # 用參數為 n=20, m=10, k=5 的超幾何分布驗證中央極限定理。
CLT(rhyper(100000, 20, 10, 5)) # 用參數為 p=0.5 的幾何分布驗證中央極限定理。
CLT(rnorm(100000)) # 用參數為 mean=0, sd=1 的標準常態分布驗證中央極限定理。
CLT(sample(1:6, 100000, replace=T)) # 用擲骰子的分布驗證中央極限定理。
CLT(sample(0:1, 100000, replace=T)) # 用丟銅板的分布驗證中央極限定理。
以下是這些指令的執行結果,從這些圖中您可以看到當樣本數到達 20 個的時候,幾乎每種樣本都會趨向常態分布。

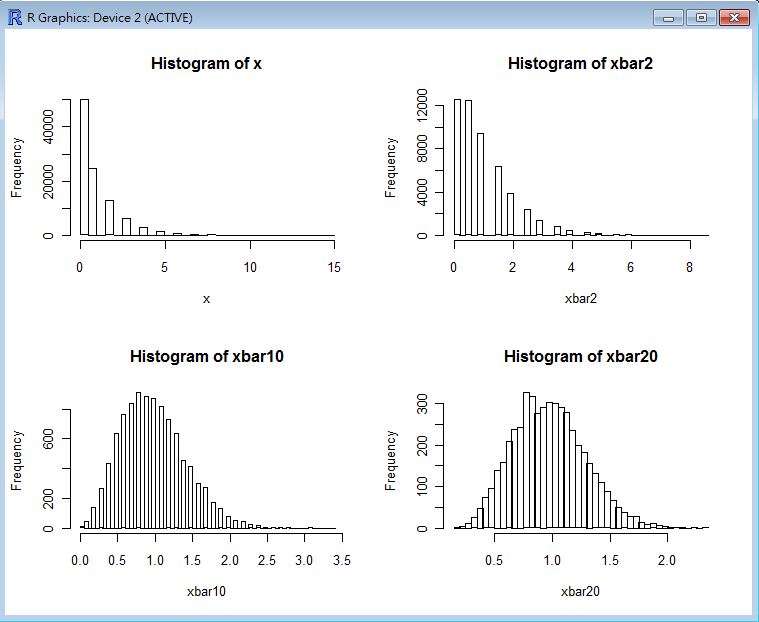

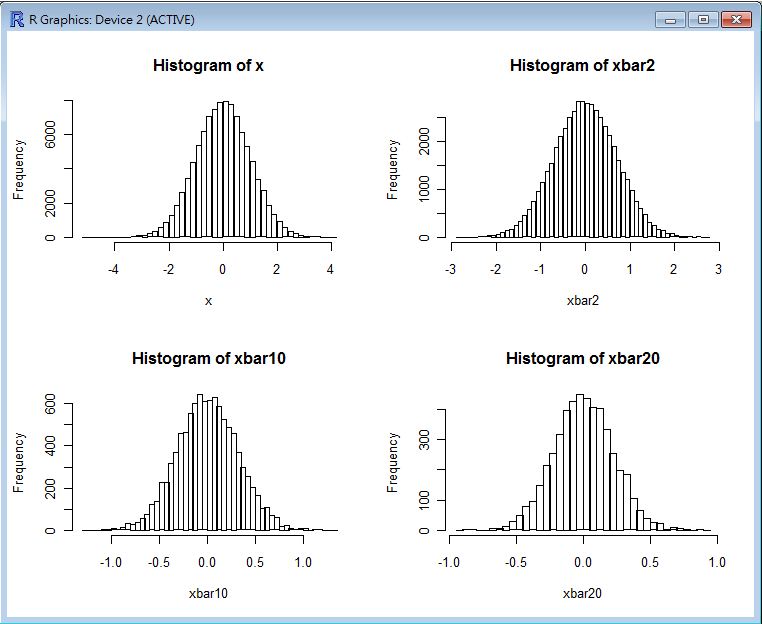
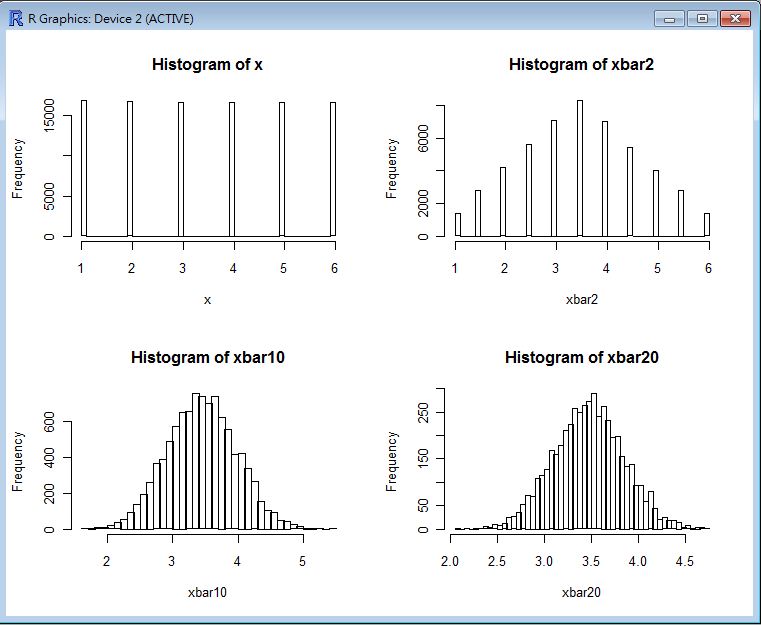
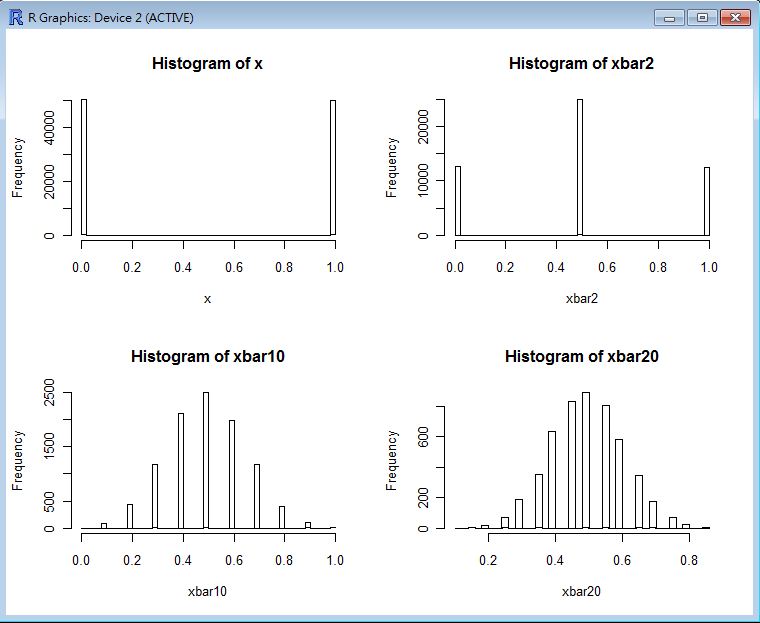
結語
在本節當中,我們沒有證明「大數法則、柴比雪夫不等式、中央極限定理」等數學定律,只用了 R 軟體來驗證中央極限定理, 如果對數學比較有興趣的同學,可以參考以下參考文獻中維基百科的證明。
參考文獻
- The Central Limit Theorem (Part 1)
- 洋洋 – 淺談機率上的幾個極限定理
- Proof of Central Limit Theorem, H. Krieger, Mathematics 157, Harvey Mudd College, Spring, 2005
- Wikipedia:Law of large numbers (有證明柴比雪夫不等式與大數法則)
- Wikipedia:Chebyshev’s inequality – http://en.wikipedia.org/wiki/Chebyshev's_inequality
- Wikipedia:Central limit theorem (有證明中央極限定理)
- 維基百科:大數定律
- 維基百科:切比雪夫不等式 (有證明柴比雪夫不等式)
- 維基百科:中央極限定理
- Two Proofs of the Central Limit Theorem, Yuval Filmus, January/February 2010